Вот хотелось провести аналогию с кубом, но что-то не заладилось. На скорую руку - возьмем путь между центрами противолежащих "граней", ну например
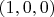
и
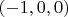
. Если провести путь как в кубе - перпендикулярно "ребрам" и через еще один центр "грани", то путь равен полупериметру фигуры

- поскольку это сечение плоскостью

. Вольфрам говорит, что это (с точностью до сотых)
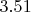
.
Но если провести "по диагонали" - к "вершинам", а затем вдоль "ребра", то это сечение плоскостью

, тогда надо считать полупериметр

, который, согласно тому же Вольфраму, равен
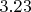
- то есть короче!
Так что аналогия с кубом плохая...
Вышеупомянутый путь может послужить (вопрос - хорошей ли) отправной точкой для поиска пути между противолежащими "вершинами". Но дальше мысль не пошла еще. Уже ясно, что искомый путь будет не длиннее. Если минимум равен

, было бы красиво...