Приношу извинения прежде всего уважаемому
Mihr, которому я, собственно, и обещал написать, что же мне не нравится в Кудрявцеве, да так и не собрался.
Много я сейчас, наверное, не напишу, однако же положим начало.
Кудрявцев несомненно хорош в том отношении, что там изложение подробное, разжёванное, неторопливое. И без явных ляпов (впрочем, я действительно въедливо его не читал, особенно в целях критики). Читать его, в целом, приятно и полезно. Особенно будущим инженерам-физикам.
Но кое-что там плохо. Прежде всего, там есть "игра в научность". Дальше ссылки по изданию 1981 г.
Например, в п.1.2 дается, в самом начале, определение того, что такое множество из одного элемента. А потом определение множества из двух элементов. А потом еще упорядоченной пары "по Куратовскому", т.е. упорядоченная пара --- это множество вида
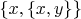
. Да трах-тарарах, зачем всё это здесь надо ? Это же книжка по матану, а не по аксиоматической теории множеств и прочим основаниям атематики. Сразу же читатель начинает думать, что высасывать из пальца какие-то тривиальности и ритуально танцевать вокруг них --- это и есть математика. Для сравнения, у Камынина написано гораздо более по-деловому: упорядоченная пара --- это множество из двух элементов, про которые указано, какой из них является первым, а какой вторым. Эти два элемента могут и совпадать.
И записывается она с помощью двух скобок и через запятую:

. Т.е. "строго" определения упорядоченной пары не дается (оно нафиг не надо), а просто максимально понятно рассказывается, что это словосочетание значит.
Да и не получилось у Кудрявцева дать это определение. Ведь, по нему, множество из двух элементов --- это

. А
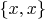
--- это множество из двух элементов, или нет ? По второму абзацу в том пункте 1.2
Кудрявцев писал(а):
Множество

называется множеством из 2-х (двух) элементов, если после вычитания из него множества, состоящего только из одного элемента

, т. е. множества, число элементов которого равно 1, останется множество, число элементов которого также равно единице. Нетрудно доказать, что это определение не зависит от выбора указанного элемента

, т. е. если

и

, причем
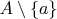
состоит из одного элемента, то и множество
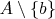
также состоит из одного элемента (а именно, из элемента

).
---нет, потому что после вычитания из
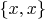
множества из одного элемента во множестве ничего не остается. Значит,
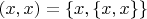
--- не упорядоченная пара. Фсё, приплыли.