Доказать, что интеграл неотрицателен.

[RikkiTan1]

Доброго времени суток!
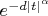
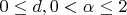
Решаю задачу по теории вероятностей. Нужно доказать, что функция $e^{-d|t|^\alpha}$ является характеристической для каждого $0\leq d, 0<\alpha\leq 2$. Решил действовать напрямую:
взять обратное преобразование Фурье и доказать, что получившаяся функция неотрицательна и интегрируема. Пока застрял на доказательстве неотрицательности.
Обратное преобразование фурье нашей функции для положительных $x$:

$$ \hat{\varphi}(x)= 2\int\limits_{0}^\infty \cos(xt)e^{-t^\alpha}dt= \sum\limits_{k=0}^\infty \int\limits_{\frac{2\pi k}{x}}^{\frac{2\pi (k+1)}{x}}\cos(xt)e^{-t^\alpha}dt= \sum\limits_{k=0}^\infty \frac{1}{x}\int\limits_{0}^{2\pi}\cos(t)e^{-\left({\frac{t+2\pi k}{x}}\right)^\alpha}dt. $$

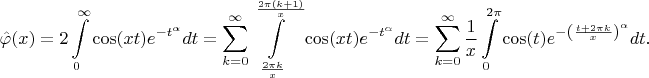
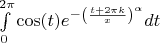
Видимо, для всех положительных $x$ интеграл $\int\limits_{0}^{2\pi}\cos(t)e^{-\left({\frac{t+2\pi k}{x}}\right)^\alpha}dt$ положителен.
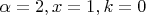
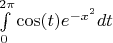
Даже если взять простой случай: $\alpha=2, x=1, k=0$, то получим выражение $\int\limits_{0}^{2\pi}\cos(t)e^{-x^2}dt$. Этот интеграл действительно положителен, но как это можно доказать не придумал. Мои знания в оценке таких выражений ограничиваются первой и второй теоремами о среднем, но с их помощью оценить не получилось.
Может быть у кого-нибудь есть идеи, как это можно оценить?

[Combat Zone]

Это тупиковый путь.

Используйте теорему Леви-Хинчина для х.ф. безгранично делимых распределений. Или сразу устойчивых, но тогда там делать будет нечего.

Насколько я помню, исторически данный результат был получен и применен именно для этой функции. Поэтому использовать его именно таким образом это читерство, конечно, а с другой стороны, альтернативный путь - додумываться, как это делал Леви или Хинчин.

При $\alpha\le 1$ можно было обойтись теоремой Пойа, но при остальных значениях параметра она не сработает.

[RikkiTan1]

Понял, спасибо. Задача состоит именно в том, чтобы доказать, что эти функции являются характеристическими напрямую, т.е. без теорем Леви-Хинчина.
Я вижу три пути, по которым можно идти:
1) доказать, что эти функции неотрицательно-определенные
2) через обратное преобразование Фурье.
3) показать, что эти функции являются поточечными пределами других характеристических функций: например функция $e^{-x^2/2}$ является х.ф., согласно ЦПТ.
Если первые два способа совсем сложные, может быть со времен Хинчина были найдены аналоги ЦПТ, но когда хар. функции стремятся не к $e^{-x^2/2}$, а к $e^{-d|t|^\alpha}$?

[Combat Zone]

Ясно. Сочувствую :)
1) выкиньте и забудьте,
3) успех маловероятен, но не запретишь,
2) тут можно что-то делать.

Наиболее современные результаты, касающиеся вашего вопроса, как раз теоремы ЛХ для устойчивых и безгранично делимых распределений. Но запрет или нежелание их использовать в этой задаче - разумное ограничение.

Неплохой обзор по этой теме есть в англовики в разделе Stable Distribution, захочется - почитаете. У вас другой вопрос.

Феллер, второй том, предоставляет целых два способа борьбы с вашей функцией.
Во-первых, там приведены плотности для устойчивых распределений, т.е. посчитано обратное преобразование Фурье, можете посмотреть. Глава 17, параграф 6. Вам осталось только убедиться в неотрицательности и восстановить пробелы.

Во-вторых, есть еще способ. Тут надо читать главу 13, преобразования Лапласа, и параграф 6 этой главы.

[Combat Zone]

Combat Zone в сообщении #1695507 писал(а):

плотности для устойчивых распределений

Звиняйте, опечатка. Плотности для нецелых значений параметров $\alpha$. В замкнутом виде они не считаются, так что приходится довольствоваться разложением в ряд.

[RikkiTan1]

Понятно. Большое спасибо за ссылки.

[Combat Zone]

RikkiTan1
Что в замкнутом виде они не считаются, не совсем верно. Очень редко считаются. Все эти результаты как раз и есть в англовики на той странице.

[Евгений Машеров]

А тут не будет достаточно теоремы Пойа?

[artempalkin]

RikkiTan1 в сообщении #1695417 писал(а):

$$ \hat{\varphi}(x)= 2\int\limits_{0}^\infty \cos(xt)e^{-t^\alpha}dt= \sum\limits_{k=0}^\infty \int\limits_{\frac{2\pi k}{x}}^{\frac{2\pi (k+1)}{x}}\cos(xt)e^{-t^\alpha}dt= \sum\limits_{k=0}^\infty \frac{1}{x}\int\limits_{0}^{2\pi}\cos(t)e^{-\left({\frac{t+2\pi k}{x}}\right)^\alpha}dt. $$

Очень мучительно это в $TeX$ будет расписывать, но разве, если рассмотреть кусочки длиной $\pi/2$, у нас не получится ряд типа Лейбница (знакопеременный с постоянно уменьшающимися по модулю членами) с первым положительным членом? Он всегда сходится (по крайней мере условно), и сумма его будет положительна.

-- 01.08.2025, 18:43 --

То есть делаем замену $xt=y$, допустим, и дальше получается так:
$[0;\pi/2]+[\pi/2;\pi]\geqslant 0$, при этом $[0;\pi/2]+[\pi/2;\pi]\geqslant |[\pi;3\pi/2]+[3\pi/2;2\pi]|$, при этом $[\pi;3\pi/2]+[3\pi/2;2\pi]\leqslant 0$ и т.д..

Это все интегралы в соответствующих пределах написаны, прошу прощения.

[Combat Zone]

Евгений Машеров в сообщении #1696057 писал(а):

А тут не будет достаточно теоремы Пойа?

Combat Zone в сообщении #1695421 писал(а):

При $\alpha\le 1$ можно было обойтись теоремой Пойа, но при остальных значениях параметра она не сработает.

(Самоцитирование есть тяжкий грех :( а что делать)
Выпуклости вниз не будет.

[Combat Zone]

artempalkin в сообщении #1696058 писал(а):

у нас не получится ряд типа Лейбница (знакопеременный с постоянно уменьшающимися по модулю членами) с первым положительным членом? Он всегда сходится (по крайней мере условно), и сумма его будет положительна.

Нет, не всегда он будет рядом Лейбница. При разных $x$ и $\alpha$ по-разному. Поиграйтесь с вольфрамом.

[Combat Zone]

artempalkin
Дошло. Вы на другие промежутки разбиваете полупрямую, на промежутки знакопостоянства косинуса. Конечно, так ряд получится знакопеременным. Но желаемого результата не получится. Приведу косвенный аргумент против. Для знакопеременности ряда достаточно, чтобы на полупрямой "характеристическая" (?) функция убывала. Но. Привести пример четной убывающей при положительных значениях аргумента функции, которая, тем не менеее, не будет характеристической, очень легко.

Почему так вышло и что ломается - посмотрите сами, если интересно.