Шутки и не шутки про порядок и хаос

[vpb]

antiDevil.ru в сообщении #1695215 писал(а):

Тут поможет диалектика. Сначала бардак, потом порядок, а потом суперпорядок, который выглядит как бардак

Конгениально ! (и это не шутка.) Вас с форума, боюсь, очень скоро удалят, но данная мысль мне нравится, и я ее тут сохраню для потомков.

[eugensk]

vpb

[Евгений Машеров]

(занудно): Конгениально это не "очень гениально", это "сходно по духу"

[Anton_Peplov]

Известная вещь: чем меньше избыточность кода, тем больше сигнал напоминает шум. Так что хорошо продуманный порядок действительно может выглядеть как хаос.
Да и вообще то, что мы не в силах понять, выглядит как бессмыслица.

[sergey zhukov]

В одной лекции недавно услышал.
Лектор рассказывал о тепловой конвекции. При разных числах Релея у нас процесс теплопереноса проходит от стадии кондуктивного теплопереноса к конвективным валам, ортогональным конвективным валам, гексагональным ячейкам и турбулентной хаотичной конвекции. И потом говорит:
- По мере роста потока тепла процесс теплопереноса от микрохаотического (кондуктивный перенос) переходит к простейшему макроупорядоченному (система валов), затем сложность упорядоченной конвективной структуры по мере роста потока тепла нарастает, и затем структура становится макрохаотической. Мы вернулсь к тому, с чего начинали (хаос), но на новом масштабе.

[chislo_avogadro]

От конгениальности до конбезумства один шаг.

[Nobody82]

Если речь идет о расстановке статических элементов в каком-то порядке, то в этом есть смысл. Все субъективно, у каждого может быть свое мнение о геометричности и симметричности расстановки предметов в квартире.

Но если речь идет про движение, то порядок - это предсказуемость. Суперпорядок - это суперпредсказуемость.

[Dendr]

Действительно, что может быть более хаотичным, чем монетка, которая миллион раз подряд выпала вверх орлом?

[Anton_Peplov]

Dendr в сообщении #1695749 писал(а):

Действительно, что может быть более хаотичным, чем монетка, которая миллион раз подряд выпала вверх орлом?

Если это комментарий к тезису "суперпорядок выглядит как хаос", то замечу, что под суперпорядком я бы подразумевал сложный порядок. А всегда выпадать орлом - это как раз очень простой порядок.

Аналогия. Простые последовательности типа $1111 \dots$ имеют низкую колмогоровскую сложность. Это простой порядок. Геном человека в двоичном виде имеет высокую колмогоровскую сложность. Это суперпорядок. Самую большую колмогоровскую сложность имеет случайная последовательность. Это хаос.

[epros]

Anton_Peplov в сообщении #1695752 писал(а):

Аналогия. Простые последовательности типа $1111 \dots$ имеют низкую колмогоровскую сложность.

Вот мне интересно, и как же конкретно Вы её считаете, эту самую колмогоровскую сложность? По моим понятиям, чтобы посчитать что-то эдакое, нужно для начала задать кучу исходных предположений, которые не самоочевидны.

[Anton_Peplov]

epros в сообщении #1695847 писал(а):

Вот мне интересно, и как же конкретно Вы её считаете, эту самую колмогоровскую сложность? По моим понятиям, чтобы посчитать что-то эдакое, нужно для начала задать кучу исходных предположений, которые не самоочевидны.

Так, как указано в книге Верещагин, Успенский, Шень. Колмогоровская сложность и алгоритмическая случайность. Более точно: я считаю простую колмогоровскую сложность относительно какого-нибудь оптимального декомпрессора. Произвол в выборе декомпрессора приводит к тому, что сложность определяется с точностью до аддитивной константы. Однако это не так важно, ибо, как пишут авторы:

Цитата:

Свойства оптимального декомпрессора, построенного при доказательстве теоремы Соломонова-Колмогорова, зависят от использованного способа записи программ (то есть от выбора языка программирования). Два таких способа приводят к сложностям, отличающимся не более чем на константу, которая есть длина интерпретатора одного языка программирования, написанного на другом языке. Можно надеяться, что при естественном выборе языков эта константа будет измеряться тысячами или даже сотнями. Тем самым, если мы говорим о сложностях порядка сотен тысяч (скажем, для текста романа) или миллионов (скажем, для ДНК), то уже не так важно, какой именно язык программирования мы выбрали.

Если совсем на пальцах, то простая колмогоровская сложность двоичной последовательности - это длина минимальной программы, печатающей эту последовательность. Аддитивная константа зависит от языка программирования. Не занимаясь деталями, сразу можно сказать, что последовательность $111111\dots 1$ кодируется двумя командами "напечатать 1 - повторить $n$ раз" (сложность $2 + C$), сложность длинной последовательности случайных блужданий с вероятностью $p \approx 1$ порядка ее длины, а геном человека где-то между этими точками.

[epros]

Anton_Peplov в сообщении #1695848 писал(а):

Не занимаясь деталями

А дьявол, как всегда, кроется в деталях. Ибо от того, как именно Вы определите "язык программирования", зависит то, что будет сжиматься, а что нет. В частности, Вы уже начали в своём примере писать какие-то операторы на естественном языке, не задумываясь над тем, что они должны быть сначала определены. На "аддитивную константу", конечно, наплевать, но строго говоря, колмогоровская сложность - это чисто воображаемая невычислимая штука. Если же Вы реально хотите получить численные оценки сложности каких-то строк, то более разумно взять какой-нибудь реальный алгоритм сжатия, например, LZW.

Вот только, рассматривая алгоритм сжатия без потерь применительно к строкам длины не более заданной, следует сразу же обратить внимание на то, что он представляет собой биекцию между конечными множествами. Отсюда следует, что если есть некое подмножество сжимаемых этим алгоритмом строк, то есть и не менее обширное подмножество строк, которые этим алгоритмом наоборот расширяются. И, надо заметить, что для реальных алгоритмов сжатия подмножество сжимаемых строк на самом деле исчезающе мало сравнительно с множеством всех возможных строк. И эти сжимаемые строки отличаются от всех прочих только тем, что мы по каким-то своим чисто субъективным причинам чаще всего пользуемся именно ими.

[druggist]

Nobody82 в сообщении #1695611 писал(а):

Но если речь идет про движение, то порядок - это предсказуемость. Суперпорядок - это суперпредсказуемость.

Странный аттрактор - детерминированная система, следовательно, суперпредсказуема на малых временах, тем не менее, демонстрирует хаос(детерминированный) на больших. Так что и в случае движения сказать, что такое порядок, не так-то просто.

[Anton_Peplov]

epros в сообщении #1695852 писал(а):

В частности, Вы уже начали в своём примере писать какие-то операторы на естественном языке, не задумываясь над тем, что они должны быть сначала определены.

Используется синтаксис C#

for (int i = 1; i <= 1000000; ++i)
out_file.WriteLine("1");
 

epros в сообщении #1695852 писал(а):

Если же Вы реально хотите получить численные оценки сложности каких-то строк, то более разумно взять какой-нибудь реальный алгоритм сжатия, например, LZW.

Нет, это не более разумно. Потому что "реальные" (читай - прикладные) алгоритмы сжатия создавались так, чтобы как можно лучше сжимать часто встречающиеся на практике последовательности, и разработчикам было плевать, что строка, которая никому никогда не встретится, при этом расширится. Задача, чтобы длина архива всегда была не больше длины исходника, не ставилась. Но такая задача разрешима, и ниже я привожу самый очевидный пример ее решения.

epros в сообщении #1695852 писал(а):

Отсюда следует, что если есть некое подмножество сжимаемых этим алгоритмом строк, то есть и не менее обширное подмножество строк, которые этим алгоритмом наоборот расширяются.

Вот алгоритм, записанный на C#, который по введенной последовательности sequence длины 100000 печатает текст программы (опять же на C#) выводящий эту последовательность. Пожалуйста, укажите последовательность, для которой количество строк в напечатанном тексте программы превзойдет длину последовательности.

Используется синтаксис C#

        int [] sequence = new int [100000];

//Опускаю заполнение массива из внешнего источника (файла, устройства, алгоритма)
        
        
int i = 0; //счетчик элементов массива
int element = sequence[0]; // запоминаем первый элемент массива
int rep = 1;  //счетчик подряд идущих одинаковых элементов

while (i < sequence.Length )
{

while(i + rep < sequence.Length &&  sequence[i + rep] == element)
++rep; //посчитали, сколько раз подряд повторяется элемент

if (rep > 1)
{
Program_text.WriteLine("for (int i = 1; i <=" + rep + "; ++i)");
Program_text.WriteLine ( "out_file.WriteLine(" + element + ");" );
//если элемент повторяется rep > 1 раз, пишем в тексте программы "напечатать его rep раз"
}
else 
Program_text.WriteLine("out_file.WriteLine(" + element + ");" ); // иначе просто пишем "напечатать этот элемент";

i = i + rep;

if (i < sequence.Length)
element = sequence[i];

rep = 1; //сбрасываем счетчик повторов
}
 

Примеры вывода программы (сократил длину массива до 10).

Для массива из одних нулей:

for (int i = 1; i <=10; ++i)
out_file.WriteLine(0);

Для массива из 5 единиц подряд, остальные нули:

for (int i = 1; i <=5; ++i)
out_file.WriteLine(1);
for (int i = 1; i <=5; ++i)
out_file.WriteLine(0);

Для массива, где 1 и 0 чередуются через один:

out_file.WriteLine(1);
out_file.WriteLine(0);
out_file.WriteLine(1);
out_file.WriteLine(0);
out_file.WriteLine(1);
out_file.WriteLine(0);
out_file.WriteLine(1);
out_file.WriteLine(0);
out_file.WriteLine(1);
out_file.WriteLine(0);

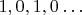
Понятно, что сжатие не оптимальное. Последовательность $1, 0, 1, 0 \dots$ можно сжать до двух строк, а мой алгоритм ее фактически не сжимает. Но любую последовательность, в которой есть хотя бы три одинаковых элемента подряд, он сжимает. И никакую не расширяет.

[Mihaylo]

epros в сообщении #1695852 писал(а):

А дьявол, как всегда, кроется в деталях. Ибо от того, как именно Вы определите "язык программирования", зависит то, что будет сжиматься, а что нет.

Да, могут быть неудобные языки для сжатия (можно синтезировать такие), но на практике обычно они достаточно удобные.

Например, можно придумать такой язык, в котором генерируется последовательность 1, 2, 3 и она может сдвигаться на чётное число позиций и суммироваться с последовательностью в памяти. Такой язык неполный и на нём хрен что закодируешь простенькое.

Плохо, что в науке такие языки не рассматривались - надо же начинать с простого...