А с чего вдруг строк? Надо в битах считать. Любую последовательность можно напечатать программой из одной строки.
epros говорит об очевидной вещи. Пусть

- инъективная функция из строк в строки. Тогда количество строк длины до

, которые она укорачивает,
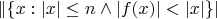
, не меньше чем количество строк длины до

, которые она удлиняет,
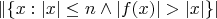
.
Да, тут я сглупил, прошу прощения. Пример с программой на C# иррелевантен. Спорить с теоремами - не мой стиль.
колмогоровская сложность как якобы однозначно определённая реально вычислимая метрика
А вот этого я, извините, не говорил. Это Вы уже домысливаете.
Колмогоровская сложность однозначно определена, только когда фиксирован оптимальный декомпрессор. Колмогоровская сложность двоичного слова

невычислима, это тоже теорема. Но при фиксированном оптимальном декомпрессоре вычислимы верхние оценки на колмогоровскую сложность относительно этого декомпрессора. Хотя бы одну точно получим. Запустим оптимальный декомпрессор

диагонально по двоичным словам возрастающей длины: сделаем первый шаг

, первый шаг

, второй шаг

, второй шаг

, первые два шага
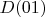
и т.д. Для всех слов

, для которых выполнение

уже завершилось, проверяем, получилось ли
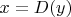
. Поскольку для оптимального декомпрессора всякое слово имеет описание, рано или поздно мы распакуем

из какого-нибудь описания

- правда, это будет не обязательно кратчайшее описание, а лишь описание, распаковка которого потребовала меньше всего шагов диагонального алгоритма. Тем не менее

будет верхней оценкой колмогоровской сложности слова

. И поскольку мы начинаем распаковку с самых коротких потенциальных описаний, при разумном выборе декомпрессора можно ожидать, что эта оценка будет не слишком завышенной. В простых примерах типа

хорошие оценки сверху легко получить вообще "на пальцах".
Да, выбор декомпрессора равносилен выбору языка. Да, сложность любой последовательности зависит от языка. И что? Весь процесс познания в той или иной степени зависит от языка.
Вот как я бы оценивал колмогоровскую сложность двоичных слов, если бы мне это понадобилось. Фиксируем удобный нам язык (равно оптимальный декомпрессор) и в нем оцениваем сверху колмогоровскую сложность любых слов. Если за разумное время не нашли оценки ниже чем длина слова, считаем, что сложность сравнима с длиной (на аддитивную константу плевать, мы можем ее директивно занулить). Это в любом случае будет так для абсолютного большинства слов. Доказано, что доля слов сложности меньше

среди всех слов длины

составляет меньше

. Например, доля слов сложности менее 90 среди всех слов длины 100 меньше

. Хорошо сжимаемые слова - это капля в море при любом выборе языка. Просто для разных языков эти капли будут разными.
Вот такой инструментальный подход. А разговоры про объективность предлагаю оставить философам.