учитывая, что выше писали, что это аж олимпиадная задача (8 класса).
Ну я там немножно погорячился, не учел условие "строго возрастающая". А насче биекции, смотрите, ведь рациональное число тоже есть упорядоченая пара целых. Но для однозначного определения люди придумали условие "взаимнопростые". Тоесть, простое число в записи

либо в числителе, либо в знаменателе, но никак и туда и сюда. А как однозначно определить число из

?
Хорошо, тогда
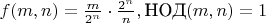
,
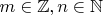
?
1. К виду

я привёл с целью получения сюръекции с простым правилом, которое, важно - обеспечивает монотонность - каждый модифицированный таким образом (домноженный) элемент из

ставится в соответствие себе же из
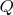
. Без домножения, как было отмечено, элементы

не имеют дробей с взаимнопростыми с двойкой знаменателями, поэтому простое правило "число из

в такое же в
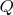
" не было бы сюръективным, поскольку

и прочие не имели бы прообраза.
Можно конечно придумать другое биективное правило: как-то пытаться выделять счётные подмножества и ими "накрывать" числа из
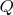
, отсутствующие в

, но нужно же ещё соблюсти монотонность, а вот это же сложновато, но подумаю ещё.
2. Ограничения на НОД пары

и

обеспечивает инъекцию, хотя опять-таки, строго доказать почему прямо сейчас не могу. Понятно, что мы исключили сокращаемость дробей, чем отсеяли множество дубликатов. Но не может ли быть двух разных несокращаемых дробей, представляющих одно и тоже число? Если нет, то почему? Может связано с основной теоремой арифметики?
И ещё есть опасения, что наложением ограничения на НОД усекли не только область определения множества пар

но и область определения - само множество

, то есть мы некоторые элементы

пропускаем.
Но это точно не целые - любой числитель

со знаменателем 1 будут удовл. условию НОД, значит все целые в области определения будут. Аналогично наоборот - при

и всеми

получим все неправильные дроби с числителем 1, аналогично для других числителей, и аналогично для правильных дробей. Ну а больше вроде ничего не остаётся в

.
3. Ограничение на натуральности

исключает неинъективность связанную с отрицательными числами, например
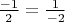
.
-- 28.07.2025, 15:40 --так писать нельзя. Потому что получится
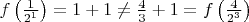
, хотя
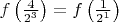
.
Ну так всё правильно, почему нельзя-то? Только в последнем равенстве нужно уточнить что это оригинальная, как Вы показали, неинъективная

, поскольку она двум разным прообразам один образ сопоставляет. Эта та функция, которой

задано.
А мы, используя эту оригинальную функцию (мы через неё "цепляемся" за элементы

), как нас просят, предъявили "инъективную" - что Вы сами и продемонстрировали, записав, что теперь эти два разных прообраза соответствуют разным образам.
Ну а в кавычках инъективная, потому что там всё равно будут дубликаты в виду сократимости, но это уже другой вопрос.