Алгебраическими системами обычно называют теории первого порядка довольно специального вида. В любом случае возникает вопрос, что такое формальные доказательства в вашем случае, это же должны быть математические объекты.
Начну издалека. Даю краткий пересказ определения интерпретации (Мендельсон (1971), с. 57 ). В Sixth edition то же самое.
Интерпретация языка первого порядка это система, в которой каждой предикатной букве
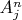
соответствует некоторое

-местное отношение в

. Всякое

-местное отношение – это подмножество ДП

, элементами которого являются

-ки элементов множества

, названного областью интерпретации.
О функциональных символах мы пока не будем говорить, так как речь идет об аксиомах, правилах вывода и многих теоремах исчисления предикатов первого порядка, в записи которых не используются функциональные символы. Это не так уж и мало. А вообще

-местный функциональный символ можно представить как

-местное отношение с определенными свойствами.
Так что можно считать, что

- это множество, а все его подмножества (т.е. интерпретации предикатов и формул) можно анализировать с использованием законов алгебры множеств по Куранту и Роббинсу, в которой помимо операций определено отношение включения. Разница лишь в том, что элементами этих множеств являются не только элементы множества

, но и

-ки элементов из

.
Вот Вам и алгебраическая система. Поскольку речь зашла о подробностях, то у меня нет иного выбора, как вести речь о конкретной алгебраической системе – об алгебре кортежей (АК), краткие сведения о которой я на днях
разместил в Интернете.
В АК традиционная интерпретация расширена. В ней предусматриваются следующие особенности:
1) определены операции, для которых доказано, что они соответствуют логическим связкам (
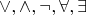
);
2) общезначимость импликации

интерпретируется как выполнимость соотношения
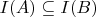
;
3) областью интерпретации является ДП
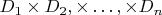
, в котором

могут быть разными множествами;
4) законы алгебры множеств по Куранту и Роббинсу верны без исключения.
Цитата:
Если обычные доказательства первого порядка, то непонятно, к чему все эти обсуждения правил вывода.
Во-первых, это не совсем обычные доказательства (см. выше), А про правило вывода могу добавить, что в АК интерпретацией упомянутого в прошлых сообщениях правила
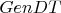
является операция добавления фиктивного атрибута, с помощью которой отношения с разными схемами отношения легко преобразуются в однотипные (т.е. имеющие одинаковые схемы отношения). И поэтому в АК нельзя с помощью интерпретации правила
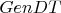
получить результат без исключений вроде
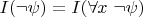
, который является интерпретацией упоминавшейся ранее «равносильности»:
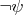
равносильно
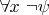
.
-- 18.07.2025, 15:39 -- Я же уже использовал её в примере, когда из
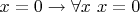
выводилось
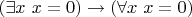
.
Ваш пример не соответствует схеме аксиом
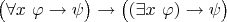
, где

не имеет свободных вхождений

, так как в этой схеме используется формула

, которая в общем случае никак не зависит от

. Допустим, она не содержит свободных вхождений

, но при этом она может не совпадать с

(например,
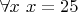
). А в Вашем примере получается
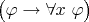
. В нем не видно формулы

, никак не связанной с формулой

.
Цитата:
Вряд ли Вы её выведете. Подсказка: квантор всеобщности должен обобщать конъюнкцию, а квантор существования - дизъюнкцию.
Я попробую доказать общезначимость формулы
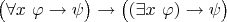
. Но не сегодня. А за подсказки спасибо. Только мне они (уж поверьте!) не нужны.