Доказательство 5-го постулата Евклида

[Konstantin12]

dgwuqtj в сообщении #1694216 писал(а):

Угол — это геометрическая фигура, образованная парой лучей с общей вершиной. В случае пары отрезков вы этот угол как-то строите или у вас другое определение?

Хорошее замечание. Спасибо!
Свое определение угла не хотелось бы громоздить.

Как вариант можно предложить, такую формулировку для построения:
Угол между лучами исходящими в противоположные стороны (т.е. угол 180 градусов) из совпадающих центров 2-х окружностей с разными радиусами и совпадающими с прямой линией, также проходящей через центры окружностей и делящей эти окружности пополам. На этих лучах расположены отрезки ограниченные точками пересечения лучей с окружностями.

Сути построения это не меняет, только удовлетворяет определению угла.

[dgwuqtj]

Замечательно, такой угол будет иметь меру $180^\circ$ и в геометрии Лобачевского. А складывать углы в разных точках всё равно нельзя.

[Konstantin12]

dgwuqtj в сообщении #1694221 писал(а):

Замечательно, такой угол будет иметь меру $180^\circ$ и в геометрии Лобачевского. А складывать углы в разных точках всё равно нельзя.

Спасибо за комментарий!

Переформулировал.


Делим окружность прямой линией ab пополам. Получаем два отрезка AO и OB с общей точкой О и углом в этой точке $180^0$
Далее строим две окружности с центрами в точках C и D, делящими эти отрезки пополам, и радиусами равными половине длины отрезков. Прямая ab также разделит эти окружности пополам.
Таким образом получаем отрезки AC, CO, OD, DB с соответствующими общими точками C, O, D в которых углы между отрезками равны $180^0$ (или, что равнозначно, $0^0$)

Так можно?

[dgwuqtj]

Можно.

[Booker48]

Konstantin12 в сообщении #1694036 писал(а):

Основная идея доказательства заключается в том, что угол между любыми отрезками, взятыми на прямой, всегда равен нулю или 180 градусам, что то же самое в данном случае.

Если данное утверждение справедливо, то верен и 5-й постулат Евклида.

Вполне возможно. Вот цитата из Погорелова "Основания геометрии", М., Наука, 1979, стр.14:

Цитата:

Существует бесчисленное множество других утверждений, с помощью которых можно было бы доказать
пятый постулат. Например:
1. Все перпендикуляры к одной стороне некоторого острого угла пересекают его другую сторону.
2. Существуют подобные и неравные треугольники.
З. Существуют треугольники сколь угодно большой площади.
4. Существуют треугольники с суммой углов, равной двум прямым.
б. Через точку вне данной прямой можно провести не более одной прямой, ей параллельной.

То бишь, эти утверждения равносильны V постулату, но, как и он, не выводятся из остальных.
Кстати, лучше не опираться в рассуждениях на аксиомы именно из "Начал", они далеки от совершенства. В частности в них про движение ничего нет, и про взаимное расположение точек (типа "лежать между"), а Евклид такими вещами в "Началах" пользуется в ряде случаев.

[Konstantin12]

Booker48 в сообщении #1694334 писал(а):

Konstantin12 в сообщении #1694036 писал(а):

Основная идея доказательства заключается в том, что угол между любыми отрезками, взятыми на прямой, всегда равен нулю или 180 градусам, что то же самое в данном случае.

Если данное утверждение справедливо, то верен и 5-й постулат Евклида.

Вполне возможно.

Спасибо за Ваш комментарий.

Booker48 в сообщении #1694334 писал(а):

Вот цитата из Погорелова "Основания геометрии", М., Наука, 1979, стр.14:

Цитата:

Существует бесчисленное множество других утверждений, с помощью которых можно было бы доказать
пятый постулат. Например:
1. Все перпендикуляры к одной стороне некоторого острого угла пересекают его другую сторону.
2. Существуют подобные и неравные треугольники.
З. Существуют треугольники сколь угодно большой площади.
4. Существуют треугольники с суммой углов, равной двум прямым.
б. Через точку вне данной прямой можно провести не более одной прямой, ей параллельной.

То бишь, эти утверждения равносильны V постулату, но, как и он, не выводятся из остальных.

Мне представляется, что у меня, вроде-как нет скрытого повторения этих утверждений.

Изучая, попытки доказательств, сделанных до меня, я пришел к выводу что проблема в том, что у моих предшественников не было "инструмента", с помощью которого можно было бы проверить "прямолинейность" прямой линии. У прямой линии всегда сохраняется возможность неконтролируемо "согнуться", т.к. отсутствуют "инструментально удобные" определения прямой линии. Да, ее можно "повесить" на двух точках, но эти точки ограничивают лишь количество прямых проводимых через эти точки. Определение прямой через вращение, отсылает к пространственной геометрии и вообще с трудом вписывается в геометрию на плоскости.
Хорошее определение прямой линии: "Прямая линия это геометрическое место точек равноудаленных от двух данных".
Но с этим определением тоже далеко не уедешь. Т.к. в момент определения расстояний включаются треугольники, а с ними подтягивается 5-й постулат.

Вот, я и решил попробовать окружностью "поджать кривизну" прямой линии. Если получить инструмент точно указывающий угол между любыми разнесенными отрезками на прямой, тогда не будет шансов задаться вопросом: "а сохранится ли угол на прямой, если мы куда-нибудь продлим прямую линию?"

Booker48 в сообщении #1694334 писал(а):

Кстати, лучше не опираться в рассуждениях на аксиомы именно из "Начал", они далеки от совершенства. В частности в них про движение ничего нет, и про взаимное расположение точек (типа "лежать между"), а Евклид такими вещами в "Началах" пользуется в ряде случаев.

Я по возможности сравниваю аксиоматику разных авторов. Просто с Евклидом, меньше возникает вопросов у читателей.
По моему мнению, у Евклида самая большая проблема с определением прямой линии, оно настолько мутное, что не понятно куда его применить. Он и сам его никуда не применяет. Так что это определение можно было бы просто выкинуть, и геометрия не заметила бы (как в прочем история это и подтвердила). Вот его определение прямой: «Прямая линия есть та, которая равно расположена по отношению к точкам на ней», что с ним делать непонятно.

-- 15.07.2025, 20:04 --

dgwuqtj в сообщении #1694296 писал(а):

Можно.

А вот так, можно говорить об угле между отрезками, обозначенными красным цветом, с учетом ранее построенных окружностей, выделенных зеленым цветом?
Сумма углов остается одной и той же, есть у отрезков общая точка или нет ее.
Или Вы считаете что без дополнительного определения, типа "разнесенного угла" не обойтись?

[dgwuqtj]

Konstantin12 в сообщении #1694348 писал(а):

А вот так, можно говорить об угле между отрезками, обозначенными красным цветом, с учетом ранее построенных окружностей, выделенных зеленым цветом?

Можно, он всё ещё нулевой. Как и угол между любыми двумя отрезками на одной прямой. Как и угол между любой прямой и ей самой, посчитанный в любой её точке.

[wrest]

Konstantin12 в сообщении #1694348 писал(а):

Если получить инструмент точно указывающий угол между любыми разнесенными отрезками на прямой, тогда не будет шансов задаться вопросом: "а сохранится ли угол на прямой, если мы куда-нибудь продлим прямую линию?"

Так вы его и не получили, этот инструмент, на мой взгляд...

[Konstantin12]

dgwuqtj в сообщении #1694349 писал(а):

Konstantin12 в сообщении #1694348 писал(а):

А вот так, можно говорить об угле между отрезками, обозначенными красным цветом, с учетом ранее построенных окружностей, выделенных зеленым цветом?

Можно, он всё ещё нулевой. Как и угол между любыми двумя отрезками на одной прямой. Как и угол между любой прямой и ей самой, посчитанный в любой её точке.

Теперь я Вас совсем не понимаю.
Сначала Вас не устраивает, что угол между любыми отрезками на одной пряной равен нулю. Вы спрашиваете как я его строю или какое у меня определение угла.
Теперь Вы повторяете за мной утверждение, что угол между любыми отрезками на прямой равен нулю.

-- 15.07.2025, 23:19 --

wrest в сообщении #1694350 писал(а):

Konstantin12 в сообщении #1694348 писал(а):

Если получить инструмент точно указывающий угол между любыми разнесенными отрезками на прямой, тогда не будет шансов задаться вопросом: "а сохранится ли угол на прямой, если мы куда-нибудь продлим прямую линию?"

Так вы его и не получили, этот инструмент, на мой взгляд...

Так тяжело вести дискуссию.
Вы вбрасываете типа: "Мне не нравиться", "Вы не получили", причем не утруждаете себя привести хоть какой-то аргумент.

- "Почему?"
- "Потому"

[Утундрий]

Да, угол между любыми двумя отрезками, лежащими на одной и той же, гностически не меняющейся по своим имманентным свойствам, прямой — равен нулю. Или ста восьмидесяти градусам, что в данном контексте не слишком чтобы значительно. И отсюда следует, что любые два отрезка, лежащие на одной прямой, все вместе и каждый по отдельности, лежат на одной прямой. А ещё эта прямая делит плоскость на две полуплоскости. И полуплоскости этих две. И между ними — прямая. Которая их делит.

[dgwuqtj]

Konstantin12 в сообщении #1694366 писал(а):

Сначала Вас не устраивает, что угол между любыми отрезками на одной пряной равен нулю. Вы спрашиваете как я его строю или какое у меня определение угла.

Меня это устраивает, я просто уточнил, мало ли что вы там называете углом. Проблема у вас в другом месте, и я первым своим сообщением написал, где конкретно.

[Null]

(Оффтоп)

Konstantin12 в сообщении #1694366 писал(а):

Вы вбрасываете типа: "Мне не нравиться", "Вы не получили", причем не утруждаете себя привести хоть какой-то аргумент.

У вас очень нестрогое расплывчатое рассуждение, соответственно вопросы будут такими же. Повторю еще раз - это вы должны объяснять что написали.

[epros]

Konstantin12 в сообщении #1694366 писал(а):

Так тяжело вести дискуссию.

Так ведь непонятно, чего Вы хотите добиться. Вот ранее я Вам уже сказал, что вместо пятого постулата можно принять за постулат, что сумма углов любого треугольника равна 180 градусам, и получить всё ту же евклидову геометрию. Судя по всему, Вы это и делаете. Зачем? Если Вас интересует доказательство для других геометрий, то имейте в виду, что в них сумма углов треугольника может быть другой.

[Konstantin12]

dgwuqtj в сообщении #1694370 писал(а):

Konstantin12 в сообщении #1694366 писал(а):

Сначала Вас не устраивает, что угол между любыми отрезками на одной пряной равен нулю. Вы спрашиваете как я его строю или какое у меня определение угла.

Меня это устраивает, я просто уточнил, мало ли что вы там называете углом. Проблема у вас в другом месте, и я первым своим сообщением написал, где конкретно.

Я, кажется, начинаю понимать в чем у Вас претензия.
И возможно у других участников претензия таже.
Просто у Вас она лучше сформулирована.

Вот Ваше 1-е сообщение (синим цветом мое выделение):

dgwuqtj в сообщении #1694187 писал(а):

Konstantin12 в сообщении #1694036 писал(а):

суммируя углы между шестью отрезками в точках A, B и C, получим сумму углов равную трем прямым, т.е. 270 градусов.

Следовательно, отрезки на сторонах CD и DA повернуты относительно друг друга на 270 градусов.

Не следовательно. Углы в разных точках не складываются.

Вот еще Ваш комментарий (синим цветом мое выделение):

dgwuqtj в сообщении #1694221 писал(а):

Замечательно, такой угол будет иметь меру $180^\circ$ и в геометрии Лобачевского. А складывать углы в разных точках всё равно нельзя.

Тогда, как быть с утверждениями о сумме углов в треугольнике?
Может они таки складываются, только проблема с суммой углов в том же треугольнике в чем то другом?
Может проблема с углами между отрезками на прямой?
Как думаете?

-- 16.07.2025, 12:22 --

epros в сообщении #1694405 писал(а):

Konstantin12 в сообщении #1694366 писал(а):

Так тяжело вести дискуссию.

...вместо пятого постулата можно принять за постулат, что сумма углов любого треугольника равна 180 градусам, и получить всё ту же евклидову геометрию.

Не спорю.

epros в сообщении #1694405 писал(а):

Судя по всему, Вы это и делаете. Зачем?

Я не пытаюсь ввести постулат, о сумме углов в треугольнике.
Я пытаюсь это доказать не опираясь на 5-й постулат.
В качестве основы использую свойство прямой, проведенной через центр окружности, делить эту окружность пополам.
И уже отсюда выводить утверждение, что угол между отрезками на прямой равен нулю.
А это в свою очередь закрывает вопрос о сумме углов в треугольнике.

Вот как я вижу проблему с углами между отрезками:

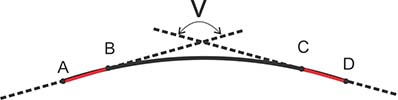
Черная сплошная линия - это прямая линия, для понимания условно изображенная искривленной.
На ней три отрезка AB, BC, CD
Углы в точках(!) между отрезками равны нулю.
Сумма углов между отрезками в точках B, C равна нулю.
Но угол между отрезками v, уже нулю не равен (продолжение отрезков условно обозначено пунктом).
Если у нас нет "инструмента" проверить равен нулю или нет угол между отрезками не имеющими общих точек на прямой, тогда мы и не можем говорить что сумма углов в треугольнике равна 180 градусов.
Я предполагаю, что нашел этот "инструмент".
Кстати, образ этого инструмента я увидел у Лобачевского, только он его пропустил мило своего внимания.

epros в сообщении #1694405 писал(а):

Если Вас интересует доказательство для других геометрий, то имейте в виду, что в них сумма углов треугольника может быть другой.

Это мне известно.

[dgwuqtj]

Konstantin12 в сообщении #1694413 писал(а):

Может они таки складываются, только проблема с суммой углов в том же треугольнике в чем то другом?
Может проблема с углами между отрезками на прямой?
Как думаете?

Я так думаю. Угол — это геометрическая фигура, у него можно ввести меру, будет некое число из $[0^\circ, 360^\circ]$ (разрешим вырожденные случаи). Меры углов складывать можно, разумеется. При этом есть есть три луча $a, b, c$ с общей вершиной, то мера угла между $a$ и $c$ будет суммой (или чем-то похожим, угол же не только парой лучей задаётся, но и выбором области) мер углов между $a$ и $b$, а также между $b$ и $c$.

Если это дело обобщать на прямые, не пересекающиеся в общей точке, то утверждение, что $\angle(a, c) = \angle(a, b) + \angle(b, c)$ в смысле мер соответствующих углов уже буквально равносильно утверждению о сумме углов треугольника (и "пятому постулату"). То есть углы между $a$ и $b$, а также между $b$ и $c$, нельзя просто сложить, чтобы найти угол между $a$ и $c$. Я писал именно об этом.

Вы угол между отрезками определяете как угловую меру угла между прямыми, содержащими эти отрезки. То есть строим прямые, находим точку пересечения (если она есть; если она не единственная, её ещё надо выбрать), выбираем лучи с этой вершиной в данных прямых и считаем меру одного из образовавшихся углов. Если отрезки на одной прямой, то всегда будет угловая мера $0^\circ$, $180^\circ$ или $360^\circ$ в зависимости от сделанных выборов. Это верно и в евклидовой геометрии, и в геометрии Лобачевского, и в сферической, и в геометрии Римана.