Разве из теоремы Михайлеску отсутствие решений не следует сразу?
Да, но есть нюанс. Как я понял из книги René Schoof, Catalan’s Conjecture (2008), в доказательстве теоремы Михайлеску случай уравнения
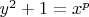
--- это отдельный случай, его требуется исследовать непосредственно. Что и было сделано V. Lebesgue'ом еще в 1850 году с помощью целых гауссовых чисел и еще кой-чего. Если и ссылаться здесь на кого-нибудь, то никак не на Михайлеску.