Это следствие манипуляций с уравнением

Т.е., расчёты/выводы были сделаны где-то (на бумаге) а Лемма 1 содержит только параметрические уравнения .Так?
Я вывожу формулы, аналогичные формулам для Пифагоровых троек. Посмотрите, как задаётся решение Пифагоровой тройки в целых числах и вы поймёте, что я вывел аналогичные соотношения
Теперь понимаю. Т.е., ищем Пифагоровы Тройки,

,

,

через известные

и

:
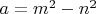
,

,

. Пусть

и

. Тогда, находим, что

,

,

, примитивная Пифагорова Тройка. У Вас-
так? Или доказано, что не
так? Если-
так, то какие есть гарантии истинности всех выводов?
3.А что об остальных

, которых целых ещё 6 штук должно быть плюс к записанному Вами,- по закону? Они тоже-корни уравнения ВТФ и, по идее, должны следовать каким-то похожим формулам, интересно. Нет?
Не понял, про какие 6 штук вы говорите
Под словами "целых ещё 6 штук" подразумевалось "аж" (т.е., " аж ещё 6 штук"), а не множество

. Т.е., если справа у Вас какое-то число , скажем,

, то оно имеет

корней:

,

,

,

,

,

,

. (При этом, как Вы помните, сумма корней равна

).
transcendent в сообщении #1690599
писал(а):
5. Вы проверяли все эти Ваши формулы в доменах выше Z?
Нет, потому что надо работать на множестве натуральных чисел
Это без разницы. Множество целых чисел,

, вложено через "ла ла ла" в множество

, p-адических целых.
Почти всё, что Вы пишете для первого множества, автоматом истинно для второго, за исключением "простых чисел" и опять же, за исключением, например, чисел, оканчивающиеся нулём, 0, в младшей позиции. Во всяком случае, всё, что касается Ваших уравнений, считайте, что Вы записали это для p-адических целых. И, тогда сообщение в цитате ниже не имеет никакого смысла:
Что число

является делителем числа 1225, а это невозможно, то есть целочисленность у меня используется
Поскольку, всегда можно рассмотреть ситуации, когда

(кстати, что это за число такое и откуда оно взялось?) будет делится на

.
Я не знаю-почему эксперты Вам перестали писать. Видимо, из-за лета? Иной причины молчания не могу представить... Но, Ваша попытка, на мой взгляд, есть классический случай, когда наглядно срабатывает p-адический контраргумент. Вот здесь это обсуждают:
https://math.stackexchange.com/questions/2288472/on-elementary-proofs-of-fermats-last-theorem Почитайте также комменты.
Извинения, если я понял что-то не так, как надо. Да и трудно это. С самого начала это написал.