Развод с теорией множеств

[EminentVictorians]

dgwuqtj в сообщении #1690473 писал(а):

а с другой — просто описать всё аксиоматически

А это тоже слышал, но не понимаю. В обычной ситуации мы можем сформулировать список аксиом, но чтобы доказать его непротиворечивость, надо потом строить теоретико-множественную модель. А в чем суть вот этого аксиоматического подхода в топосах? Т.е. моделью является не множество, а топос?

[dgwuqtj]

Раз аксиомы накладываются на сам топос, то он и будет моделью. А с чего вы взяли, что это не множество? Ну или класс. Скажем, категория пучков на сайте является множеством, если аккуратно ограничить мощности.

И в такой деятельности непротиворечивость специально доказывать не надо, так как обычно уже есть хотя бы одна модель, ради которой аксиомы и придумывают.

[EminentVictorians]

dgwuqtj в сообщении #1690515 писал(а):

А с чего вы взяли, что это не множество?

Я похоже запутался... Мне казалось, что у нас базовая теория - это какая-нибудь теория категорий с неопределяемыми понятиями типа объектов, стрелок, композиции. Понятия множество и элемент множества - определяемые. Множество - это объект топоса Set. Элемент множества A - это морфизм из терминального объекта 1 в A. Сам топос Set определяется чисто на языке теории категорий.

Мне казалось, что весь цимес всех этих синтетических теорий - это что мы можем сформулировать аксиомы, которые мы хотим, а затем беспроблемно построить топосную модель для этих аксиом. Другими словами, вот сформулировали мы странный набор аксиом, где у нас все функции бесконечно гладкие, производные вычисляются просто делением бесконечно малых, и любая функция локально - в точности маленький отрезок прямой (а не как в стандартном матанализе, где функция линеаризуется лишь с точностью до бесконечно малой более высокого порядка, чем само приращение). Построить теоретико множественную модель этого списка аксиом не получится: либо нереально, либо слишком сложно. А "теоретико топосная" строится на ура. А значит можно не париться относительно противоречивости этих аксиом и делать матанализ в духе Лопиталя, просто единственное следить, чтобы логика интуиционистская была (ибо топос). Или я вообще все не так понял?

dgwuqtj в сообщении #1690515 писал(а):

И в такой деятельности непротиворечивость специально доказывать не надо, так как обычно уже есть хотя бы одна модель, ради которой аксиомы и придумывают.

Хм.. а мне казалось наоборот, что аксиомы есть, а подходящей теоретико-множественной модели нету. Вот мы и строим в качестве модели топос, т.к. это проще.

[dgwuqtj]

EminentVictorians в сообщении #1690518 писал(а):

Мне казалось, что у нас базовая теория - это какая-нибудь теория категорий с неопределяемыми понятиями типа объектов, стрелок, композиции. Понятия множество и элемент множества - определяемые. Множество - это объект топоса Set. Элемент множества A - это морфизм из терминального объекта 1 в A. Сам топос Set определяется чисто на языке теории категорий.

А при чём тут синтетическая дифференциальная геометрия? Она на основания не претендует. Чтобы делать основания так, как вы пишете, нужно кучу аксиом на теорию категорий, чтобы строить новые топосы, я таких не видел. Кучу в том смысле, что захочется теорему полноты для интуиционистской логики: у любой непротиворечивой теории существуют топос и модель в этом топосе.

EminentVictorians в сообщении #1690518 писал(а):

мы можем сформулировать аксиомы, которые мы хотим, а затем беспроблемно построить топосную модель для этих аксиом.

Если аксиомы первого порядка, никто не мешает взять теоретико-множественную модель (для классической логики) или шкалу Крипке (для интуиционистской логики; это тоже некий теоретико-множественный конструкт, естественно). Нужна всего лишь подходящая теорема о полноте.

EminentVictorians в сообщении #1690518 писал(а):

А значит можно не париться относительно противоречивости этих аксиом и делать матанализ в духе Лопиталя, просто единственное следить, чтобы логика интуиционистская была (ибо топос).

Вы говорите про использование формального вывода для доказательства чего-то про объекты гладких топосов. Так можно, это как использовать формальный вывод для доказательства теоретико-групповых тождеств вида $[x, y z] = [x, y]\,{}^y[x, z]$. То есть такой способ доказательств будет неким переусложнением, хотя с опытом существование формального вывода можно начать доказывать неформально, как обычно и делают в литературе.

EminentVictorians в сообщении #1690518 писал(а):

Хм.. а мне казалось наоборот, что аксиомы есть, а подходящей теоретико-множественной модели нету. Вот мы и строим в качестве модели топос, т.к. это проще.

А вы вообще видели эти аксиомы? Это просто условия на топос, и мне неочевидно, можно ли их сформулировать через внутреннюю логику. Конечно, модель таких аксиом — это некая категория, она спокойно строится в ZFC. И сам топос основанием математики служить не может, в нём даже натуральные числа не предполагаются.

[EminentVictorians]

dgwuqtj в сообщении #1690526 писал(а):

А при чём тут синтетическая дифференциальная геометрия? Она на основания не претендует.

Так об этом ведь даже речи не было. В качестве оснований я думал, что теория категорий.

dgwuqtj в сообщении #1690526 писал(а):

Так можно, это как использовать формальный вывод для доказательства теоретико-групповых тождеств вида $[x, y z] = [x, y]\,{}^y[x, z]$.

Формальный вывод - это имеется в виду такая цепочка?

$$[x, y z] = xyzx^{-1}(yz)^{-1} = xyzx^{-1}z^{-1}y^{-1} = xyx^{-1}y^{-1}yxzx^{-1}z^{-1}y^{-1} = [x, y]\,{}^y[x, z]$$

Я чувствую какую-то аналогию между доказательствами в интуиционистской логике и такими вычислениями, но не могу сформулировать. Наверное дело в соответствии Карри-Ховарда.

dgwuqtj в сообщении #1690526 писал(а):

То есть такой способ доказательств будет неким переусложнением, хотя с опытом существование формального вывода можно начать доказывать неформально, как обычно и делают в литературе.

Так почему переусложнением? Разве не в том цель и заключается, чтобы вместо использования деталей конструкции (хоть топоса, хоть множества) использовать внутренний язык, который беднее (как я и хочу)?

dgwuqtj в сообщении #1690526 писал(а):

Это просто условия на топос, и мне неочевидно, можно ли их сформулировать через внутреннюю логику.

Я думал, что аксиомы сначала формулируются на внутреннем языке, а потом под них строится топос - модель этих аксиом. Ну и этот топос как бы оправдывает возможность использования этих аксиом.

[dgwuqtj]

EminentVictorians в сообщении #1690621 писал(а):

Я думал, что аксиомы сначала формулируются на внутреннем языке, а потом под них строится топос - модель этих аксиом. Ну и этот топос как бы оправдывает возможность использования этих аксиом.

Я всё-таки открыл книжки Kock, Synthetic differential geometry и Synthetic geometry of manifolds. Вы правы. Только топос, который строится, специально выбирается так, чтобы применяться к обычным гладким многообразиям.

EminentVictorians в сообщении #1690621 писал(а):

Формальный вывод - это имеется в виду такая цепочка?

А вы умеете это переписывать в виде дерева вывода в естественном выводе или исчислении секвенций? Конечно, студенты-математики это изучают в курсе матлогики, но к тому моменту они и с простенькой дифференциальной геометрией работают.

Просто при изучении классической математики, без матлогики и категорий, достаточно интуитивного понимания доказательств. А при использовании этих техник сначала нужно доказать, что формальный вывод работает в топосах (или где нам нужно), а потом — что неформальные рассуждения можно формализовать. С опытом, конечно, на это мысленных усилий тратить не придётся, ну так и к классическим $\varepsilon$-$\delta$-рассуждениям тоже легко выработать привычку, там даже пререквизитов на порядок меньше.

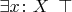
Кстати, обычно матлогику так излагают, что формула $\exists x \colon X \enskip \top$ становится истинной (где $X$ — это сорт $x$, в приложении к топосам нужна логика с многими сортами). Вы понимаете, что для интерпретации в топосах это неверно и что надо поправить в определении формального вывода?

EminentVictorians в сообщении #1690621 писал(а):

Так почему переусложнением? Разве не в том цель и заключается, чтобы вместо использования деталей конструкции (хоть топоса, хоть множества) использовать внутренний язык, который беднее (как я и хочу)?

Потому что больше пререквизитов! Вместо матанализа в объёме 3 семестров и, скажем, теории меры придётся учить основы теории категорий, потом матлогику (включая интуиционистский естественный вывод с многими сортами переменных), потом что-то про топосы. Даже если по объёму текста это может быть сопоставимо, во втором случае определения сложнее мотивировать. Это как сравнивать доказательства основной теоремы арифметики (при помощи кратной индукции, без абстракций) и леммы Йонеды для семиклассника. Плюс для практических приложений всей этой высокой науки не хватит и придётся доучивать тот самый матанализ. Вот вы можете найти преимущества синтетического подхода при вычислении элемента площади псевдосферы?

[EminentVictorians]

dgwuqtj в сообщении #1690629 писал(а):

А вы умеете это переписывать в виде дерева вывода в естественном выводе или исчислении секвенций?

Нет, а это надо уметь? Меня просто формальная логика в принципе напрягает.

Я большими усилиями над собой вроде бы научился перестраиваться на интуиционистскую логику. Это уже великое достижение для меня. Но разумеется я имею в виду обычные неформализованные доказательства в интуиционистской логике (на таком же уровне строгости, как обычные неформализованные доказательства на классической логике из обычных учебников по математике).

dgwuqtj в сообщении #1690629 писал(а):

Вот вы можете найти преимущества синтетического подхода при вычислении элемента площади псевдосферы?

Меня бесполезно спрашивать такие вещи, я вообще матанализ применять не умею, ни классический, ни синтетический. Теорию освоить получилось относительно легко (я про одномерный анализ больше, многомерный не знаю), а вот с практикой беда. Меня, к слову, сами эпсилон-дельта рассуждения не особо напрягают. Меня больше всего раздражает теоретико-множественный язык, который слишком сильный и позволяет задавать всякие странные вопросы, конструировать бессмысленные функции и тп. Это противоречит моей философии. Я хочу, чтобы язык был слабый и чтобы было сложно моделировать предметную область (а рассуждать дальше в ней - легко). С теорией множеств наоброт - моделировать легко, а дальше рассуждать в ней сложно. Вот я и надеюсь на все эти топосы: теорию категорий мне понять гораздо проще, чем классический матанализ, а топосы - это кандидаты на маленькие теории с бедными внутренними языками (как мне и хочется).

[dgwuqtj]

EminentVictorians в сообщении #1690703 писал(а):

Я хочу, чтобы язык был слабый и чтобы было сложно моделировать предметную область (а рассуждать дальше в ней - легко).

SDG это делает, но только по отношению к каким-то общим определениям. Если открыть хоть учебник по геометрии кривых, хоть препринт про кэлеровы многообразия, вам одной только SDG точно не хватит.

-- 16.06.2025, 12:06 --

В чём тогда смысл, если нельзя будет понять даже формулировки содержательных теорем, не говоря уже про доказательства?

[epros]

EminentVictorians в сообщении #1690421 писал(а):

Теория множеств провоцирует платонизм.

А может это платонизм спровоцировал теорию множеств? Судя по всему, создатели теории множеств и её первые поклонники и были платонистами, так что не удивительно, что математика в их понимании получила такое развитие.

EminentVictorians в сообщении #1690421 писал(а):

Как тогда можно однозначно утверждать, что какое-то утверждение либо истинно, либо ложно?

Вот этот вопрос имеет ли какое-то отношение к теории множеств? Брауэр, судя по всему, не захотел принять не столько теорию множеств, сколько платоновское понимание "истинности" - он сходу заявил, что истинным может считаться только то, что доказано, и разговоры о каких-то истинах, якобы существующих независимо от наших знаний, недопустимы.

[EminentVictorians]

dgwuqtj в сообщении #1690709 писал(а):

SDG это делает, но только по отношению к каким-то общим определениям.

И если взять SIA (кусок SDG нацеленный чисто на анализ), то оказывается, что в нем формулируются все основные теоремы матана: производная суммы, разности, произведения, частного, композиции; что производная интеграла с переменным верхним пределом равна подынтегральной функции (теорема Барроу), производная в точке внутреннего экстремума равна нулю (теорема Ферма), что если производная ноль, то функция константа (а значит, что если производные одинаковы, то функции отличаются на константу) и так далее. А это лишь то, что я по приколу подоказывал буквально за 1 вечер. Доказательства настолько простые, что их можно школьникам давать.У меня такое ощущение, что всё ядро матанализа в SIA есть. Да, нету например, теорем типа Кантора-Бенедиксона. Но где она реально используется, например, для каких-то вычислений? По-моему, нигде. Эта теорема (и ей подобные) - это, имхо, в чистом виде артефакт теории множеств. К самому сферическому матанализу в вакууме (существующему вне рамок конкретных формализаций типа теоретико-множественной) такие теоремы отношения не имеют.

dgwuqtj в сообщении #1690709 писал(а):

Если открыть хоть учебник по геометрии кривых, хоть препринт про кэлеровы многообразия, вам одной только SDG точно не хватит.

Вот только оставаясь в теории множеств, мне наверное жизни не хватит, чтобы даже дойти до этих кэлеровых многообразий. Может быть, синтетические теории - это шанс для таких как я хоть что-то понять в математике.

dgwuqtj в сообщении #1690709 писал(а):

В чём тогда смысл, если нельзя будет понять даже формулировки содержательных теорем, не говоря уже про доказательства?

Ну, пример SIA показывает, что очень большая часть (если вообще не все) содержательные теоремы (одномерного - потому что это единственное, о чем я могу говорить) анализа остаются. Кстати, это интересный момент. Мне кажется, такое ощущение будет преследовать все синтетические теории в сравнении с их теоретико-множественными аналогами. Из-за самой природы синтетической математики. Синтетические теории "выворачивают наружу" аксиомы. По сути они как бы выкидывают лишнюю шелуху (теоретико-множественные детали) и оставляют самый сок. Поэтому кажется, что такие теории всегда будут оставлять впечатление выжимки самых содержательных теорем (просто потому что психика так устроена - люди реально создают теории для гораздо меньшей области применимости, чем им позволяет теория множеств; матанализ создавался не для того, чтобы анализировать функции Дирихле или Римана).