Чтобы было удобнее рисовать рисунки и писать формулы, рассмотрим в ИСО-с-ноликом (

не бесконечно малый элемент объёма, а ящик с конечным объёмом

где

- длина ребра, параллельного х-оси,

- ширина вдоль y-оси,

- высота вдоль z-оси. При преобразованиях Лоренца (ПЛ) вдоль х-оси не будут меняться поперечные размеры

ящика и координаты


любых точек, поэтому за ними дальше не следим. Объём

ящика преобразуется как его длина

Формулы преобразования длины (и тем самым объёма) ящика выведем с помощью формул ПЛ.
0. Пусть
в ИСО-с-ноликом ящик всё время покоится. Ниже на рисунке его положение в момент времени
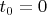
показано чёрным жирным отрезком длиной

Концы отрезка обозначены как мировые точки

и

Чтобы не плодилось много букв, обозначаю мировые точки так же, как значения их х-координаты в заранее указанной системе отсчёта.
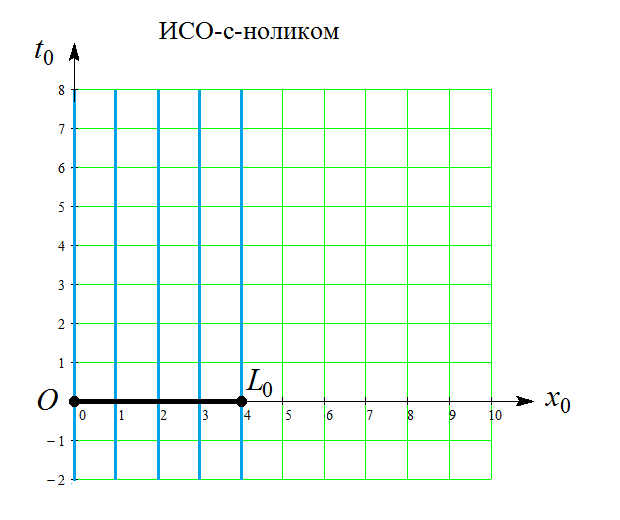
Для наглядности на ребре ящика нанесены риски с метками 0, 1, 2, 3, 4. Мировые линии этих рисок на этом рисунке и на следующих рисунках изображены синими линиями.
Мировая точка

принята за начало отсчёта, её 4-координаты равны нулю во всех обсуждаемых здесь системах отсчёта. Координаты мировой точки

в ИСО-с-ноликом есть

и

- это собственная длина х-ребра ящика, она же - длина отрезка

на рисунке.
На рисунках в численном примере указано значение

и рассматриваются два ПЛ в другие системы отсчёта со скоростями
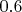
(как в примере с тест-вопросом в предыдущем сообщении). Этих данных достаточно для численной проверки рисунков; поэтому численные подсчёты координат мировых точек по формулам ПЛ не выписываю.
1. Пусть
в ИСО-просто (

тот же ящик вместе с ИСО-с-ноликом выглядит движущимся вдоль х-оси со скоростью

Вот картина при положительном значении

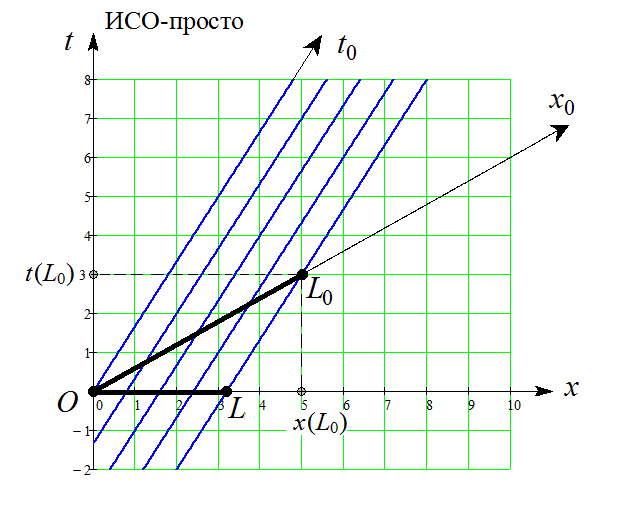
Положение ящика на х-оси в ИСО-просто в момент времени

изображается отрезком

Нам надо найти его длину

Видно, что для этого достаточно из координаты

вычесть расстояние

где

и

это координаты мировой точки

в новой системе отсчёта, т.е. в ИСО-просто.
Если задана скорость новой ИСО, измеренная в старой ИСО, то в формулы ПЛ для новых координат эта скорость входит со знаком минус. У нас же задана скорость

старой системы отсчёта, измеренная в новой (в ИСО-просто). Ясно что при этом (и с условием, что направления пространственных осей обеих систем одинаковы) скорость новой ИСО, измеренная в старой (в ИСО-с-ноликом) есть

и поэтому в формулы ПЛ она у нас входит как



Таким образом:

Другими словами: ящик объёмом

покоящийся в ИСО-с-ноликом, движется в ИСО-просто со скоростью

При этом измеряемый в ИСО-просто его объём

есть

Определение объёма

основано на измерении х-координат обоих концов х-ребра ящика в один и тот же момент времени

Кажущееся удивительным с бытовой точки зрения "лоренцево сокращение длины", т.е. несовпадение

с

(и, как следствие, различие

и

объясняется, как видим, тем, что из-за относительности одновременности велич
ины

и

оказываются длинами двух
разных отрезков в пространстве-времени.
2. Пусть
в ИСО-штрих (

ИСО-просто (

выглядит движущейся вдоль х-оси со скоростью

Вот картина при положительном значении

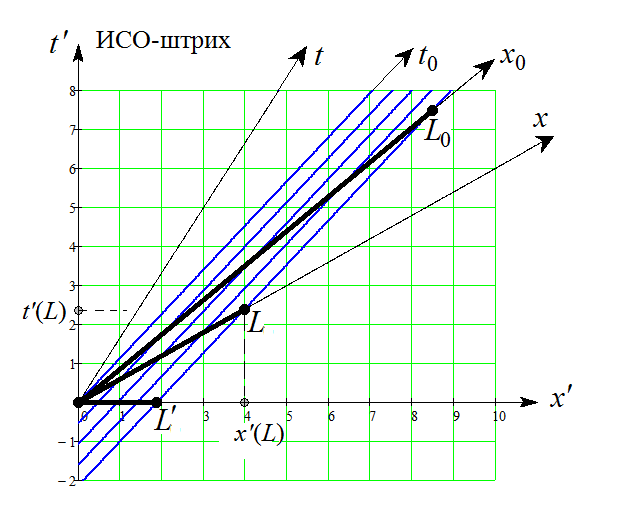
По формулам ПЛ штрихованные координаты точки

есть


Чтобы найти длину

ящика, измеренную в ИСО-штрих, как видно, достаточно из координаты

вычесть расстояние

где, однако, скорость

это не скорость

ИСО-просто в ИСО-штрих, а скорость ящика в ИСО-штрих:

Таким образом:

Другими словами: ящик объёмом

движущийся в ИСО-просто со скоростью

движется в ИСО-щтрих со скоростью

где

- скорость ИСО-просто, и при этом измеряемый в ИСО-штрих объём

этого ящика есть

Речь здесь идёт о движениях, параллельных одному и тому же направлению;

и

- значения скоростей со знаком.
(ТС не дал ответа на тестовый вопрос из предыдущего сообщения. Приведённые пояснения с рисунками, думаю, делают ответ очевидным: если элемент объёма

считать движущимся в ИСО-с-ноликом, то все предложенные в тест-вопросе варианты неправильные; если

покоится в ИСО-с-ноликом, то правильный результат:
