Электростатическое поле с геометрической точки зрения

[igodima]

Здравствуйте, уважаемые форумчане!

Известно, что с геометрической точки зрения электромагнитный потенциал представляет собой компоненты локальной формы связности $A_i$ тривиального главного расслоения $P=R^{1,3}\times U(1)$. Данные компоненты преобразуются по правилу ${A_i}' = A_i + d_ia$, которое лежит в основе соответствующей калибровочной теории и объясняет инвариантность наблюдаемых величин, таких как Е и В.

У меня возник вопрос. А можно ли с помощью подобного геометрического подхода описать макроскопическое электростатическое поле $\varphi$? Насколько я понимаю (возможно, ошибаюсь), в этом случае может иметь место только глобальная симметрия, т.е. в каждой точке пространства к значению потенциала мы можем прибавить только одно и то же число, поскольку разность потенциалов - величина наблюдаемая и не может быть произвольно изменена.

Тогда по аналогии можно рассмотреть тривиальное главное расслоение $E = R^3 \times R$ (здесь $R$ - группа трансляций). Форма связности в этом расслоении будет иметь вид $\omega = dx\omega_x + dy\omega_y + dz\omega_z + d\varphi$, а соответствующие компоненты равны $\omega_x = - d_x\varphi$, $\omega_y = - d_y\varphi$, $\omega_z = - d_z\varphi$. Подобное расслоение, только над двумерной базой, подробно рассмотрено у М.О. Катанаева в его "Геометрических методах математической физики". Как нетрудно заметить, в этом случае компоненты формы связности совпадают с компонентами векторного поля Е, т.е. описывают напряженность электростатического поля.

Интересно мнение специалистов. Сам я любитель, поэтому тапками прошу сильно не кидать

[Утундрий]

Для начала поправьте формулы.

[igodima]

Ну вот, только нашел, как знак частной производной вставлять, а тут бац вторая смена... Не дает больше править. В общем, выражения вида $d_i$ - это $\partial_i$, а $R$ - это $\mathbb R$. Приношу извинения

[Утундрий]

Зиер гут, Вольдемар. Едем дальше:

igodima в сообщении #1625288 писал(а):

можно ли с помощью подобного геометрического подхода описать макроскопическое электростатическое поле $\varphi$? Насколько я понимаю (возможно, ошибаюсь), в этом случае может иметь место только глобальная симметрия,

Вероятней всего, здесь наблюдается крайне неудачный набор букв. Макроскопическое, в пику микроскопическому, обычно означает тем или иным способом усреднённое. Поясните, что здесь имеете в виду?

Так-то, микроскопически, электростатическое поле является частным случаем электродинамического и никаких новых формулоначертаний не требует.

[pppppppo_98]

а в чем смысл тривиальной (нулевой) формы... вообще связность возникает для того что был какой-то метод сравнивать слои над разными точками база (ПВ) - ведь этоже же дифференциальная геометрия, и что такое пренести слой - понятие далеко не интуитивное. Вот и приходит на выручку связность - правило как сравнивать слои (и стало быть дает возможность измерения эволюции). А для чего нужна связность в электростатическом случае. ну есть в каждой точке потенциал - поле скалярное, перенос тривиальный (на любой разумной топологии многообразии)

[igodima]

pppppppo_98 в сообщении #1625307 писал(а):

а в чем смысл тривиальной (нулевой) формы...

Из того, что я читал, в релятивистских теориях поля, где пространство-время отождествляется с пространством Минковского, в квантовой механике при описании эффекта Ааронова-Бома, в ситуации с монополем Дирака и еще ряде случаев используется тривиальное расслоение. При этом сама U(1) связность может быть и нетривиальной.

Конкретно мне это нужно, чтобы попытаться приложить в одной не совсем физической области. А геометрический подход как раз и привлекает своей абстрактностью, способностью описывать как физические, так и нефизические объекты. Гипотезы измышляю, в общем

-- 09.01.2024, 11:45 --

Утундрий в сообщении #1625302 писал(а):

Вероятней всего, здесь наблюдается крайне неудачный набор букв. Макроскопическое, в пику микроскопическому, обычно означает тем или иным способом усреднённое. Поясните, что здесь имеете в виду?

Имеется ввиду попытка геометрического описания электростатического поля в веществе.

[Утундрий]

igodima в сообщении #1625335 писал(а):

Имеется ввиду попытка геометрического описания электростатического поля в веществе.

Для этого нужно, как минимум, геометрически описать само вещество. И тут я могу только пожелать всех и всяческих успехов. Трупы предшественников - вон там.

[pppppppo_98]

igodima в сообщении #1625335 писал(а):

А геометрический подход как раз и привлекает своей абстрактностью, способностью описывать как физические, так и нефизические объекты.

а обыкновенный тензорно алгебраический (как в ладавшице и прочих букварях по калибровочным теориям) вас не устраивает?

Утундрий в сообщении #1625357 писал(а):

геометрически описать само вещество.

не ну есть же струны (правда от самого начального подхода остается только едва заметная оболчка - я как то слабо могу себе визуально представить геометическое пространство в котором 26 измерений для правых мод и 10мерное простанство для левых мод)... но в целом наверное как-то можно... списывать в трупы струны - оснований нет , как соственно нетэкспериметнальной проверки ее следствий в обозримом будущем

[igodima]

pppppppo_98 в сообщении #1625383 писал(а):

не ну есть же струны

Зачем сразу струны Электродинамика сплошной среды в геометрическом аспекте имеет место быть. Например, есть соответствующий раздел у Коноплевой и Попова в их ""Калибровочных полях" и обширный список литературы в приложении к нему. Но там рассматривается искривленное пространство, к которому добавляется еще и тензор кручения, компоненты которого описывают источники поля. Математика получается совершенно неподъемной, наверное, даже для большинства людей с профильным образованием, не говоря уже о простых смертных. Хотелось бы чего-нить попроще и по-наглядней.

[igodima]

Ввиду отсутствия содержательных комментариев и возможного непонимания о чем речь, распишу более подробно.

Потенциал в любой точке электростатического поля может быть получен путем сложения потенциалов отдельных зарядов, создающих это поле. Будем рассматривать "макроскопический" случай, когда элементарных зарядов много, а расстояние между ними пренебрежимо мало, так что их распределение можно считать непрерывным. Создаваемое ими суммарное поле описывается достаточно гладкой скалярной функцией $\varphi$. Для простоты и наглядности рассмотрим одномерный случай $\varphi=f(x)$.

Расслоение. На график данной функции можно посмотреть, как на сечение тривиального главного расслоения $E = \mathbb R \times \mathbb R $. Данное расслоение представляет собой обычную плоскость ${\mathbb R}^2$ с декартовой системой координат $x, \varphi$, в которой ось абсцисс (база) - это физическое пространство, ось ординат (слой) - абстрактное внутреннее пространство состояний, а вся плоскость (пространство расслоения) - фазовое пространство динамической системы.

Касательное пространство. В любой точке $p \in E$ касательное пространство $T_p(E)$ к пространству расслоения представляет собой такую же плоскость ${\mathbb R}^2$, начало координат которой совпадает с точкой $p$, а ось ординат является его вертикальным подпространством $V_p(E)$.

Связность. Зададим в расслоении E связность, то есть инвариантное распределение горизонтальных подпространств $H_p(E)$. Поскольку расслоение тривиально, то сделать это можно следующим образом - сначала задать связность на имеющемся сечении, а затем разнести ее по всему пространству расслоения с помощью группового действия. Пусть точка $p \in E$ лежит на графике функции $\varphi=f(x)$. Отождествим горизонтальное подпространство $H_p(E)$ в точке $p \in E$ с касательной к графику в данной точке. Если провести касательные ко всем точкам графика, то мы зададим связность на имеющемся сечении главного расслоения $Е$.



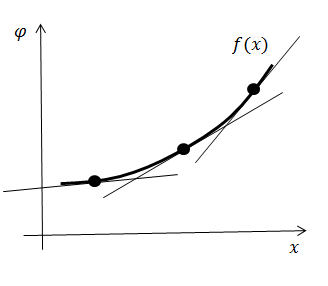
Теперь будем сдвигать полученную конструкцию на все возможные векторы вдоль вертикальной оси и отождествим распределение горизонтальных подпространств с касательными ко всем точкам каждой из полученных кривых. По построению такое распределение будет инвариантно относительно трансляций. Также потребуем выполнение неравенства $\frac{\partial\varphi}{\partial x} \ne \infty$. Это является необходимым и достаточным условием для разложения касательного пространства в каждой точке $p \in E$ в прямую сумму вертикальных и горизонтальных подпространств $T_p(E) = V_p(E) \bigoplus H_p(E)$. Тем самым мы задали связность $\Gamma$ в расслоении $E$.

Касательный вектор. Рассмотрим вектор $X$, касательный к пространству расслоения (обычный вектор на плоскости), в координатном базисе $X = X^x {\partial}_x + X^\varphi {\partial}_\varphi$. Он раскладывается единственным образом на вертикальную и горизонтальную составляющие $X = vX + hX$, где

$vX = X^\varphi {\partial}_\varphi - X^x \frac{\partial\varphi}{\partial x} {\partial}_\varphi$,

$hX = X^x{\partial}_x + X^x \frac{\partial\varphi}{\partial x} {\partial}_\varphi$.



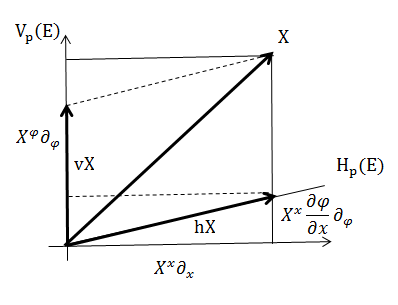Форма связности. Упрощенно говоря, в рассматриваемом случае это 1-форма $\omega : {\mathbb R}^2 \to \mathbb R$, ставящее в соответствие каждому касательному вектору $X$ его вертикальную компоненту $vX$. Форма связности однозначно определяет распределение горизонтальных подпространств и, следовательно, связность $\Gamma$ в расслоении $E$. Действительно, если известны два вектора $X$ и $vX$, то всегда можно найти третий вектор $hX$, а, значит, и все горизонтальное подпространство $H_p(E)$. Как и любая 1-форма форма связности может быть представлена в виде $\omega = dx {\omega}_x + d\varphi$, где $dx$ и $d\varphi$ - дифференциалы координат вектора в дуальном пространстве 1-форм, а ${\omega}_x$ - вещественная компонента, дифференцируемо зависящая от точки $x \in \mathbb R$. Исходя из вышеприведенного разложения вектора $X$ на вертикальную и горизонтальную составляющую, данная компонента равна:

${\omega}_x = - \frac{\partial\varphi}{\partial x}$.

Как известно, электростатический потенциал определен с точностью до произвольной константы. Это означает, что если мы добавим или вычтем постоянное значение из потенциала во всех точках пространства, то поле и все его свойства останутся неизменными. В данной геометрической модели это свойство реализуется за счет трансляционной инвариантности - при сдвигании графика по вертикали производная в каждой его точке остается неизменной. При этом компонента формы связности ${\omega}_x$ совпадает с компонентой векторного поля $E_x$ и описывает напряженность электростатического поля E.

-- 10.01.2024, 22:47 --

Уважаемые коллеги! Хотелось бы получить комментарии по существу: "да, это корректное описание", "нет, это ахинея, потому, что...". С восклицаниями типа "а зачем это нужно..." и "а не проще ли..." просьба проходить мимо. Спасибо за понимание

[Утундрий]

Вместо всец этой тонны букв и символов можно было сказать примерно следующее. Мы присобачили к пространству Минковского пятое измерение и отложили вдоль него скалярный потенциал. Нобелевку сюда!

[igodima]

По аналогии можно рассмотреть потенциал, каким он видится с точки зрения калибровочной теории. Для наглядности также ограничимся одним физическим измерением. Теперь в качестве модели будет выступать поверхность бесконечного цилиндра единичного радиуса, образующая которого (прямая $\mathbb R$) – это база, физическое пространство, а направляющая (единичная окружность $S^1$) – слой, представляющий собой мультипликативную группу Ли комплексных чисел, равных по модулю единице. Данная группа обозначается $U(1)$ и реализуется элементами вида $g = e^{i\theta}$. Таким образом, мы получили тривиальное главное расслоение $P = \mathbb R \times U(1)$.

Касательное пространство к пространству расслоения в точке $p \in P$ представляет собой плоскость, которая проходит ровно через одну образующую, содержащую данную точку. Связность на данном расслоении задается так же, как и в вышерассмотренном случае. Сначала выбирается некоторое сечение – кривая $g(x) = e^{iy(x)}$ на поверхности цилиндра. При этом функция $y = f(x)$, параметризующая данную кривую, принимает значения в интервале $[0, 2 \pi]$, концы которого отождествлены. Ко всем точкам этой кривой проводятся касательные, которые отождествляются с горизонтальными подпространствами. Затем полученная конструкция вращается вокруг оси цилиндра на все возможные углы, в результате чего и получается связность – распределение горизонтальных подпространств, инвариантное относительно группового действия.



Потенциал в данной модели отождествляется с компонентой локальной формы связности $A_x$. Для этого задается произвольное сечение $\sigma(x) = e^{i \alpha (x)}$, $\alpha \in [0, 2 \pi]$. Дифференциал данного сечения отображает вектор $X$, касательный к базе, в вектор $\sigma X$, касательный к пространству расслоения, следующим образом. Как видно из рисунка, приращению аргумента $\partial x$ соответствует приращение параметра $\alpha$.



Если $\partial x$ стремится к нулю, то дуга $\partial \alpha$ переходит в бесконечно малый отрезок на касательной плоскости, такой что:

$$\sigma X = X^x{\partial}_x + X^x\frac{\partial \alpha }{\partial x} {\partial}_y$$

При этом вертикальная компонента вектора $\sigma X$ будет равна:

$$v(\sigma X) = X^x\frac{\partial \alpha }{\partial x} {\partial}_y - X^x\frac{\partial y}{\partial x} {\partial}_y = X^x\frac{\partial (\alpha-y)}{\partial x} {\partial}_y$$

По определению в рассматриваемом случае локальная форма связности $\omega_{\sigma}$ на векторе $X$ принимается равной форме связности на векторе $\sigma X$: $\omega_{\sigma}(X) = \omega (\sigma X) = dxA_x$, откуда следует выражение для компоненты локальной формы связности:

$$A_x = \frac{\partial (\alpha-y)}{\partial x}$$

Если имеется другое сечение $\sigma’(x) = e^{i \alpha’ (x)}$, такое что $\varphi (x) = \alpha’ (x) - \alpha (x)$, то потенциал $A_x$ будет изменяться по правилу:

$${A’}_x = A_x + {\partial}_x \varphi $$

Действительно:

$$A_x = \frac{\partial \alpha}{\partial x} - \frac{\partial y}{\partial x}$$

$${A’}_x = \frac{\partial \alpha'}{\partial x} - \frac{\partial y}{\partial x}$$

откуда:

$${A’}_x - A_x = \frac{\partial \alpha'}{\partial x} - \frac{\partial \alpha}{\partial x} = \frac{\partial (\alpha' - \alpha)}{\partial x} = \frac{\partial \varphi}{\partial x} = {\partial}_x \varphi$$

Наглядно это видно на рисунке, где при повороте на угол $\varphi $ вектор еще дополнительно доворачивается на дугу, которая и будет равна $\partial \varphi$.



Данное преобразование потенциала является калибровочным, поскольку параметр преобразования $\varphi (x)$ дифференцируемо зависит от точки пространства-времени. Его можно рассматривать как переход от одного сечения к другому либо как сдвиг точек расслоения под действием структурной группы. При этом сама форма связности, отождествляемая с электромагнитным полем, вообще никак не преобразуется, поскольку задана на пространстве расслоения еще до рассмотрения каких-либо сечений.

[Утундрий]

igodima
Вы действительно не понимаете насколько это всё тривиально? Прекратите извергать из себя псевдоматематический понос и явно сформулируйте предмет обсуждения.

[igodima]

Утундрий в сообщении #1625688 писал(а):

извергать из себя псевдоматематический понос

Вы себе не слишком ли много позволяете, уважаемый Заслуженный участник? То свои неудовлетворенные влажные фантазии о Нобелевке на меня проецируете, то теперь вот проблемы с пищеварением. А на счет тривиальности - так у вас же вещество еще не описано с геометрической точки зрения. Уверены, что все правильно понимаете?

Тема обсуждения - корректность предложенных наглядных иллюстраций электростатического потенциала. Да, простенько, но не все же здесь д.ф.-м.н.? Или все? Если все, и модераторы сочтут тему недостойной нахождения на данном форуме - пожалуйста, пусть сносят. Если же нет, то еще раз прошу Вас, Утундрий, персонально, проходите мимо.

P.S. И в каком, кстати, месте Вы у меня псевдоматематику увидели? Каждое предложение готов подкрепить ссылкой из литературы. Просто еще не значит тривиально и тем более псевдонаучно.

[Утундрий]

igodima
Ещё (и последний) раз спрашиваю: в чём предмет обсуждения? Иллюстрации свойств графика функции путём изображения графика функции с учётом её свойств - не предлагать. Воздержитесь от дальнейших излияний букв, пока не ответите на этот вопрос. Считайте это требованием ЗУ.