Напряженность над полосовой доменной структурой (ПДС)

[GAA]

В разделе Magnetic field above the FGF работы
A.V. Straube and P. Tierno “Synchronous vs. asynchronous transport of a paramagnetic particle in a modulated ratchet potential”, EPL, 103, 2013 (см. в прикреплении)
рассматривается поле над поверхностью «бесконечно толстой плёнки», т.е. в предположении, что толщина $h$ плёнки много больше периода $\lambda$ доменов вдоль оси $x$. При выводе выражения, на мой взгляд (в деталях разобраться не смог), допущены опечатки

Цитата:

The choice $M(x,t) = \pm 2M_s$ ensures that $H_z^{sub} = \pm M_s$.

Должно быть $M(x,t) = \pm M_s/2$.

Цитата:

For the substrate field, we find $H^{sub}(w) = -\partial_w \Phi^{sub}(w) = -(2M_s/\pi) \sum_{n=-\infty}^{\infty} [\ln(w-x_n^+) - \ln(w-x_n^-)]$.

Потерян множитель 2.
В результате вычислений получен результат в два раза больше правильного.

1. Для поверки я нашел решение задачи в виде тригонометрического ряда

$\Delta \psi = 0$, $ \frac {\partial \psi(x,0)} {\partial z} = M(x)/2.$

$$M(x) = \begin{cases} M_s, & 2kd < x< (2k+1)d;\\ -M_s, & (2k+1)d < x<2(k+1)d.\\ \end{cases}$$

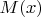
Здесь $d = \lambda/2$. Так как функция $M(x)$ периодична с периодом $\lambda$ и нечётная, а решение убывает к нулю при $z \to +\infty$, то оно ищется в виде
$\psi_n(x,z) = A_n\sin\frac {n\pi x}{d}\exp\left(-\frac{ n\pi x }{d}\right)$.
И получается
$\psi(x, z) = -\sum\limits_{k=0}^{+\infty} \frac {2M_sd}{\pi^2 (2k+1)^2} \sin\frac{(2k+1)\pi x}{d}\exp\left(\frac {(2k+1)\pi z}{d}\right)$.
Отсюда
$H_x = -\frac {\partial \psi} {\partial x} = \frac {2M_s} {\pi} \sum\limits_{k=0}^{+\infty}\frac 1 {2k+1} \cos\frac {(2k+1)\pi x}{d} \exp\left(\frac{(2k+1)\pi z}{d}\right)$.

2. Другой способ нахождения поля над ПДС
Можно записать потенциал одного полосового домена конечной длины и высоты $h$
$\psi (r) = \frac {M_s}{4\pi} \int_V \frac {z-z’}{\left( (x-x’)^2 +(y -y’)^2 + (z-z’)^2\right)^{3/2}} dx’dy’dz’$.
Потом устремить его длину к бесконечности, дифференцированием найти в элементарных функциях $H_x$ и $H_z$ , а затем сложить такие $H_x$ и $H_z$ от разных доменов.
________________________
На рис. ниже для высоты $z = 0.000001$м (1мкм), M = 10000, $\lambda = 0.00001$м (10мкм) и $h = 0.1$м рассчитаны значения вторым способом RHx, RHz (число доменов равно 10), Hz_s — первым способом и Hx_inf, Hz_inf по выражению статьи. Начало отсчета выбрано в центре (первого в способе 2) домена.

Вложение:

Pic1.PNG

Видно, что значения, найденные по выражению статьи, приблизительно в два раза больше значений, полученных разложением в тригонометрический ряд. После уменьшения величины потенциала статьи в два раза, значения, найденные по способу 2, и значения, найденные по выражению в статье, почти совпадают. Значения, полученные разложением в ряд, совпадают со значениями, найденными по выражению в статье.

Вложение:

Pic2.PNG

Вопрос: правильно ли указаны мною опечатки в выводе в статье?

[Alex-Yu]

GAA в сообщении #1601813 писал(а):

Вопрос: правильно ли указаны мною опечатки в выводе в статье?

Вряд ли кто-то станет с этой двойкой разбираться. Это только для тех, кого этот очень частный вопрос интересует профессионально. Добавлю еще, что это очень похвально, что вы не верите статьям на слово и проверяете то, что там написано.

[GAA]

В предыдущем моём сообщении находились значения напряженности без внешнего поля. Поэтому $\Delta(t)=0$.

Используя разложение $\psi$ в ряд, можно найти
$H_z = -\frac{\partial \psi}{\partial z} = - \frac{2M} {\pi} \sum\limits_{k=0}^{+\infty}\frac{1}{2k+1}\sin\frac {(2k+1)\pi x}{d}e^{-\frac {(2k+1)\pi z}{d}}$.

Вводя $H = H_x - iH_y$, можно вычислить сумму ряда $H$
$H = \frac{2M} {\pi} \sum\limits_{k=0}^{+\infty}\frac 1{2k+1}e^{\frac {(2k+1)\pi(ix-z)}d} = -\frac M {\pi} \ln \frac {1-u }{1+u}$,
где $u=e^{ \frac{i\pi}{d} w }$. Это выражение совпадает с точность до коэффициента 2 с выражением в статье (если внешние поля отсутствуют и учитывая $d=\lambda/2$).

Вложение:

Pic3.PNG

Т.е. вопрос об опечатке в статье в краевом условии.