Здравствуйте. Мне стало интересно попробовать доказать, что существует бесконечно много простых близнецов. Не могли бы вы оценить:
Начнем с утверждений:
Цитата:
Есть биекция между натуральными числами из промежутка
![$[2,p]$ $[2,p]$](https://dxdy-03.korotkov.co.uk/f/6/4/6/646df6f588b0b2ada5c4054263d8bfa182.png)
и их остатками от деления на все простые числа

, где p - простое число.
Это легко следует из китайской теоремы об остатках.
Поэтому давайте вместо чисел представлять массивы из этих остатков.
Далее отсюда легко видеть, что:
Цитата:
Число является простым тогда и только тогда, когда в таком представлении все элементы массива не равны

.
Очевидно, т.к. простое число не может делиться на другое простое.
Далее давайте рассмотрим отрезок натуральных чисел
![$[p+1,2p], p \rightarrow \infty$ $[p+1,2p], p \rightarrow \infty$](https://dxdy-04.korotkov.co.uk/f/7/7/b/77b3ebe0280c4dcfea7786615397840782.png)
, где

простое. Давайте докажем, что на этом отрезке обязательно будут простые близнецы.
Для этого заметим, что у первого близнеца остаток от деления на

равен

, а от деления на остальные простые числа

(давайте здесь числа на данном отрезке будем представлять в виде массивов из остатков на простые до

) не равен

и

. Это следует из того, что число близнец при прибавлении к нему

должно оставаться простым.
Далее утверждение, которое понадобится дальше:
Цитата:
На любом отрезке из натуральных чисел длиной

(праймориал) и левым концом

(простое число) находятся все массивы из остатков без повторений.
Это следует из биекции между числами и массивами остатков (опять же китайская теорема об остатках).
Давайте теперь вернемся на отрезок
![$[p+1,2p], p \rightarrow \infty$ $[p+1,2p], p \rightarrow \infty$](https://dxdy-04.korotkov.co.uk/f/7/7/b/77b3ebe0280c4dcfea7786615397840782.png)
, где

простое. В нем, как видно, находится гораздо меньше чисел, чем на отрезке длиной в праймориал

.
Зафиксируемся на нечетном числе

и пройдем по всему отрезку с шагом

. На каждом шаге, мы к каждому остатку

в массиве, соответствующему предыдущему числу, прибавляем

по модулю соответствующего простого числа

. Далее я делаю интуитивное предположение, что т.к. на каждом шаге массивы отличаются от массивов на предыдущем шаге, то предлагаю приблизить данный массив массивом случайных натуральных чисел. Такое предположение можно сделать, т.к. на шаге

значения

массива, соответсвующие простым числам

, где

меняются друг относительно друга беспорядочно. А для

значения остатков

еще достаточно малы относительно

.
Прошу, дайте оценку данному предположению, пожалуйста.
Далее давайте найдем вероятность того, что на

ом шаге какое-то

будет равно 0 или

(либо число не простое, либо не близнец). Она равна

Далее найдем вероятность того, что на каждом из
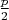
шагов мы получим не близнеца:

, а это я запрограмировал и нашел, что стремится к нулю.
Значит вероятность не найти близнеца на данном отрезке стремится к нулю.
ч.т.д
Я вижу, что слабое место как раз в предположении, поэтому прошу раскритиковать, где я не прав.
UPD:
Я предполагаю, наверное, что если взять отрезок
![$[p+1,2p], p \rightarrow \infty$ $[p+1,2p], p \rightarrow \infty$](https://dxdy-04.korotkov.co.uk/f/7/7/b/77b3ebe0280c4dcfea7786615397840782.png)
, где

простое, но вместо начала

взять

, где

- случайная величина много меньше

. Тогда все остатки будут случайными числами.