Хм. Если мысленно раскрыть скобки в правой части и перенести туда левую, то получится тождество вида

с какими-то коэффициентами

(причём, очевидно,

и
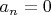
, но не в этом суть; вернее, не совсем в этом). А в том, что это -- дифференциальное уравнение Эйлера для функции

:

Решениями такого уравнения являются функции

, но только в том случае, когда

является корнем характеристического уравнения. Но дело в том, что любая функция

(уж во всяком случай при нецелых

) исходному тождеству удовлетворяет. А это означает, что и характеристическое уравнение является тождеством, т.е. все

, вот и всё.