Так, извиняюсь, неверно сформулировал.
Попытаюсь пояснить:
Случайные величины

каждая принимает одно значение -

либо

.


Вероятность того, что ровно одна любая

примет значение

, математическое ожидание

Вероятность того, что ровно две любые

примут значение

, математическое ожидание
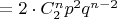
Ровно три, матожидание:

и так далее
Сумма всех математических ожиданий вышеуказанных с.в.

т.е. формула из учебного пособия.
Но чтобы получить математическое ожидание случайной величины, которая принимает хотя бы одно любое значение

из

, надо точно также сложить все математические ожидания случайных величин - ровно одной, принимающей значение

, ровно двух, принимающих значение

каждая и так далее.
Таким образом, математическое ожидание с.в.

, которая принимает значения

с вероятностью

равно математическому ожиданию случайной величины, которая принимает хотя бы одно любое значение

из

.