... в этом частном случае есть решение попроще (во всяком случае, без уравнений Пелля).
Без него никак ) Последний пример:

.



Отсюда два Пелля:

Смешно, конечно, но
mathematician123, вопрос-то знакомый, где же взять для Вас по каждому поводу доказательств? Решения Пелля образуют последовательности подобные Люка, делимость по любому модулю периодична, и каждый член, начиная с некоторого номера имеет "собственный" простой делитель (первое вхождение). Даже квадраты при таких условиях встречаются разве что в ранних номерах, а тут нужно чтобы степени (в том числе и собственных делителей) образовались сразу в числителе и знаменателе подх. дроби. Но это ладно, тут у нас кроме всего прочего еще и не одно решение, а целых два! Расположим их как в последовательности подходящих дробей:

Игреки Пелля образуют последовательность

и оказываются все кратны

из-за нуля в начале. В нашем случае знаменатели взаимно просты

, значит
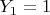
. Это может быть только если

— квадрат без единицы. Сделаем подстановку

Не понимаю пока что это дает, просто повод для размышления. Короткий период может быть выписан в общем виде:

Ага. При таком раскладе последовательность

образует уже строго последовательность Люка

Тут из

следует

, поэтому степень простого может быть только под простым номером. Наименьший член кратный заданному модулю может быть найден алгоритмом
https://dxdy.ru/post1335809.html#p1335809, как для Фибоначчи:

и т.д., но степень

кроме

не встречал. Что из этого следует — может, Вам быстрее в голову придет. Отвечать на посты, кстати, было бы вежливо с Вашей стороны.