Если вопрос в том, как могут появиться многочлены степени

, то, например,
можно рассмотреть авторегрессионный дискретный процесс, например, третьего порядка:

где

- случайная ошибка.
Если интересно узнать, при каких параметрах

этот процесс является стационарным,
то есть, при


не разлетается на бесконечность,
то нужно выяснить, при каких значениях параметров

все корни

уравнения многочлена 3-й степени
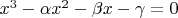
находятся внутри единичного круга на комплексной плоскости.
Эту область стационарности, то есть, множество таких

, можно посмотреть здесь
https://www.geogebra.org/m/e7jdmedu