VAL, спасибо. Давайте разбираться предметно.
Я свои программы приводил
здесь. В них есть ошибки?
Не знаю. Меня, например, смущает округление в задаче, где все изначально целочисленно.
Цитата:
И конечно предлагаю взглянуть на Ваши программы и на результаты их работы.
Пожалуйста.
Вот для 8 паттернов с 98 на 11-м месте (это maple, а не PARI):
Код:
restart; with(combinat); with(NumberTheory);
S := permute([17, 19, 23, 29, 31, 37]);
for ii from 31 by 90 to 720 do P := S[ii]; print(P); M := [P[1]^2, 2*P[2]^2, 3*P[3]^2, 2^2, 5*P[4]^2, 2*3^2, 7*13^2, 2^5, 3*11^2, 2*5^2, P[5]^2, 3*2^2, P[6]^2, 2*7^2, 5*3^2]; for i to 15 do m || i := M[i] end do; a := 2*P[2]^2; mm := 6*ilcm(op(M))/a; print(cat('a', " ="), a); print(cat('m', " ="), mm); r1 := rhs(op(msolve(a*x-1, m1))); r2 := rhs(op(msolve(a*x+1, (1/3)*m3))); r3 := rhs(op(msolve(a*x+3, (1/5)*m5))); r4 := rhs(op(msolve(a*x-5, 27))); r5 := rhs(op(msolve(a*x+5, (1/7)*m7))); r6 := rhs(op([msolve(a*x-26, 64)][1])); r7 := rhs(op(msolve(a*x+7, (1/3)*m9))); r8 := rhs(op(msolve(a*x+8, (1/2)*m10))); r9 := rhs(op(msolve(a*x+9, m11))); r10 := rhs(op(msolve(a*x+11, m13))); r11 := rhs(op(msolve(a*x+12, (1/2)*m14))); p1 := chrem([seq(r || i, i = 1 .. 11)], [m1, (1/3)*m3, (1/5)*m5, 27, (1/7)*m7, 64, (1/3)*m9, (1/2)*m10, m11, m13, (1/2)*m14]); print(cat('p1', " ="), p1); E := [[5, 10], [7, 14], [11, 9], [13, 7], [P[1], 1], [P[3], 3], [P[4], 5], [P[2], 2], [P[5], 11], [P[6], 13]]; W := []; for b in E do for j from 0 do q := (a*(j*mm+p1)+b[2]-2)/b[1]^2; if `mod`(q, b[1]) = 0 then break end if end do; W := [op(W), [b[1], j]] end do; print(sort(W)); print(M[3], M[5]); print(14000+ii); T := [seq(0, i = 1 .. 15)]; for i to 15 do for j from 100000000000 to 100000010000 do if tau(a*(j*mm+p1)+i-2) = 12 then T[i] := T[i]+1 end if end do end do; print(T); t := mul(s, s in T)/10.^60; print(t, 1/t); print() end do;
А вот вывод:
Код:
[17, 23, 29, 19, 31, 37]
a =, 1058
m =, 2498329881229038838581600
p1 =, 4490201041996487392891549
[[5, 3], [7, 0], [11, 5], [13, 10], [17, 14], [19, 16], [23, 11], [29, 11], [31, 21], [37, 19]]
2523, 1805
14031
[2302, 814, 773, 2347, 782, 776, 830, 800, 735, 659, 2321, 779, 2382, 694, 782]
-15 14
1.550787150 10 , 6.448338187 10
[19, 17, 23, 29, 31, 37]
a =, 578
m =, 4573067498858690469237600
p1 =, 7042158276307918213642189
[[5, 0], [7, 1], [11, 8], [13, 1], [17, 0], [19, 7], [23, 5], [29, 19], [31, 12], [37, 28]]
1587, 4205
14121
[2387, 781, 784, 2355, 826, 786, 761, 802, 734, 669, 2456, 827, 2413, 679, 775]
-15 14
1.727256731 10 , 5.789527301 10
[19, 31, 37, 17, 23, 29]
a =, 1922
m =, 1375251308189554157762400
p1 =, 706510592256678820525261
[[5, 2], [7, 5], [11, 2], [13, 11], [17, 12], [19, 6], [23, 16], [29, 16], [31, 19], [37, 3]]
4107, 1445
14211
[2376, 794, 827, 2396, 812, 775, 716, 713, 732, 625, 2319, 778, 2372, 673, 793]
-15 14
1.254856100 10 , 7.969041231 10
[23, 29, 31, 17, 19, 37]
a =, 1682
m =, 1571482172616125500130400
p1 =, 2950952235732722963586181
[[5, 1], [7, 1], [11, 8], [13, 1], [17, 7], [19, 11], [23, 11], [29, 4], [31, 13], [37, 34]]
2883, 1445
14301
[2378, 759, 840, 2340, 726, 785, 720, 791, 741, 655, 2310, 727, 2389, 666, 765]
-15 14
1.142409326 10 , 8.753429942 10
[29, 19, 23, 17, 31, 37]
a =, 722
m =, 3660987554487982120802400
p1 =, 23269416888858390477061
[[5, 4], [7, 2], [11, 1], [13, 3], [17, 0], [19, 5], [23, 0], [29, 16], [31, 23], [37, 6]]
1587, 1445
14391
[2364, 749, 791, 2405, 746, 876, 761, 760, 730, 644, 2458, 817, 2299, 700, 810]
-15 14
1.566739272 10 , 6.382682925 10
[31, 17, 19, 23, 29, 37]
a =, 578
m =, 4573067498858690469237600
p1 =, 950850093312928522906189
[[5, 0], [7, 2], [11, 4], [13, 3], [17, 12], [19, 2], [23, 21], [29, 16], [31, 2], [37, 8]]
1083, 2645
14481
[2378, 790, 806, 2358, 834, 780, 767, 763, 724, 646, 2366, 756, 2445, 690, 804]
-15 14
1.542374947 10 , 6.483507800 10
[31, 29, 37, 17, 19, 23]
a =, 1682
m =, 1571482172616125500130400
p1 =, 1435836264660139229331781
[[5, 2], [7, 0], [11, 2], [13, 7], [17, 8], [19, 4], [23, 13], [29, 16], [31, 24], [37, 18]]
4107, 1445
14571
[2438, 847, 766, 2451, 838, 779, 753, 810, 750, 640, 2385, 807, 2376, 672, 831]
-15 14
1.892215312 10 , 5.284810844 10
[37, 23, 29, 17, 19, 31]
a =, 1058
m =, 2498329881229038838581600
p1 =, 3911229542632454810083549
[[5, 3], [7, 3], [11, 3], [13, 6], [17, 6], [19, 1], [23, 6], [29, 28], [31, 26], [37, 1]]
2523, 1445
14661
[2405, 860, 806, 2366, 789, 807, 766, 795, 739, 602, 2336, 752, 2399, 724, 779]
-15 14
1.617140042 10 , 6.183756348 10
Для паттернов с 28 на 4-м месте программа аналогична. Только
Код:
M := [P[1]^2, 2*P[2]^2, 3*P[3]^2, 7*2^2, 5*P[4]^2, 2*3^2, 11^2, 2^5, 3*P[5]^2, 2*5^2, 7^2, 3*2^2, 13^2, 2*P[6]^2, 5*3^2]
А вот ее вывод
Код:
[2384, 789, 794, 814, 799, 793, 2201, 762, 793, 607, 2113, 792, 2299, 754, 766]
Действительно для 28 подходящих случаев больше (814 против примерно 700). Но далеко не в 8 раз.

 , ни
, ни 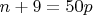 .
. 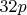 . Как же не выполнено?
. Как же не выполнено? и
и  .
. ,
,  ,
,  ,
,  и
и  .
. может быть поставлена уже двумя способами для каждой из двух вышеприведённых базовых расстановок. То есть всего 4 способа. Но, согласно моим последним исследованиям, они
может быть поставлена уже двумя способами для каждой из двух вышеприведённых базовых расстановок. То есть всего 4 способа. Но, согласно моим последним исследованиям, они 
 и
и 

 и
и 
 и
и 
 ,
,  и
и 
 вариантов паттерна.
вариантов паттерна. и
и  , а теперь занимаюсь сравнением
, а теперь занимаюсь сравнением  и
и  .
. , то начинайте его хотя бы со
, то начинайте его хотя бы со  , а лучше ещё сильно дальше). Иначе получите сильно искажённую статистику. Сам на это натыкался.
, а лучше ещё сильно дальше). Иначе получите сильно искажённую статистику. Сам на это натыкался. ).
). . И от
. И от  до
до  миллиардов нашлось
миллиардов нашлось  шестёрок простых при проверке по
шестёрок простых при проверке по  шестёрка при проверке по
шестёрка при проверке по 
 или, тем более, ровно на
или, тем более, ровно на  . А на числовой оси такие места есть только вблизи чисел кратных
. А на числовой оси такие места есть только вблизи чисел кратных  . Вот и получается, что наши планеты удалены не дальше чем на 7 единиц от центральной звезды. Они равны
. Вот и получается, что наши планеты удалены не дальше чем на 7 единиц от центральной звезды. Они равны  .
. моя программа занимает 53с, вместе с PARI 58с.
моя программа занимает 53с, вместе с PARI 58с.