Ряд операторов

[sirin0880]

Здравствуйте. Столкнулся со следующей проблемой. Пусть имеем линейный оператор на плоскости в стандартном базисе $(1,0)^T$ и $(0,1)^T$, который задаётся матрицей
$A = \begin{pmatrix} a&a \\ a&a \end{pmatrix}$
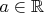
где $a\in\mathbb{R}$ - параметр.
Далее, пусть $S =\sum\limits_{n = 0}^{\infty}A^n$
Найдите чему равен $S$ при $a = 0.25$.

Как я понял, сходимость этого ряда операторов - это сходимость сумм $a_{ij}$ элементов матриц.
Для начала я нашёл общую формулу для элемента матрицы пользуясь следующими рассуждениями:

$\begin{pmatrix} a&a \\ a&a \end{pmatrix} * \begin{pmatrix} a&a \\ a&a \end{pmatrix} = \begin{pmatrix} 2a^2&2a^2 \\ 2a^2&2a^2 \end{pmatrix}$

Далее

$\begin{pmatrix} 2a^2&2a^2 \\ 2a^2&2a^2 \end{pmatrix} * \begin{pmatrix} a&a \\ a&a \end{pmatrix} = \begin{pmatrix} 4a^3&4a^3 \\ 4a^3&4a^3 \end{pmatrix}$

Таким образом формула для элемента матрицы S имеет следующую формулу:

$$s_{ij} = \sum\limits_{n = 0}^{\infty}2^na^n$$

При $a = 0.25$ имеем:

$$s_{ij} = \sum\limits_{n = 0}^{\infty}2^n*\frac{1}{4^n} = \sum\limits_{n = 0}^{\infty}\frac{1}{2^n} = 2$$

.

Но это неправильный ответ. Помогите, пожалуйста, разобраться в чём ошибка.

[mihaild]

sirin0880 в сообщении #1505481 писал(а):

сходимость этого ряда операторов - это сходимость сумм $a_{ij}$ элементов матриц

Не совсем - обычно это либо сходимость по норме, либо сходимость на каждом векторе. Но для конечномерного случая это всё одно и то же.

sirin0880 в сообщении #1505481 писал(а):

$s_{ij} = \sum\limits_{n = 0}^{\infty}2^na^n$

Вот это неверно.
Общий вид матрицы $A^n$ напишите.

[nnosipov]

sirin0880 в сообщении #1505481 писал(а):

Помогите, пожалуйста, разобраться в чём ошибка.

Во-первых, писать $*$ вместо знака умножения --- это вульгарно некрасиво. Во-вторых, чему равно $A^0$?

[Slav-27]

Можно поменять базис так, что матрица будет $\begin{pmatrix}2a&0\\0&0\end{pmatrix}$. (Вообще это стандартный алгоритм вычисления функций от операторов.)

[sirin0880]

mihaild в сообщении #1505482 писал(а):

sirin0880 в сообщении #1505481 писал(а):

сходимость этого ряда операторов - это сходимость сумм $a_{ij}$ элементов матриц

Не совсем - обычно это либо сходимость по норме, либо сходимость на каждом векторе. Но для конечномерного случая это всё одно и то же.

sirin0880 в сообщении #1505481 писал(а):

$s_{ij} = \sum\limits_{n = 0}^{\infty}2^na^n$

Вот это неверно.
Общий вид матрицы $A^n$ напишите.

Да, по поводу сходимости не так выразился. если ряд операторов сходится, то элементы матрицы, которая равна этому ряду, сходятся к сумме соответствующих элементов. Общий вид такой (если неправильно, то не могу понять почему...):
$A^n = \begin{pmatrix} (2a)^n&(2a)^n\\ (2a)^n& (2a)^n\\ \end{pmatrix}$

[mihaild]

sirin0880 в сообщении #1505583 писал(а):

Общий вид такой (если неправильно, то не могу понять почему...)

nnosipov в сообщении #1505483 писал(а):

чему равно $A^0$?

[sirin0880]

nnosipov в сообщении #1505483 писал(а):

Во-вторых, чему равно $A^0$?

Об это совсем забыл. Т.к. $A^0 = I$, т.е.

$$\begin{pmatrix} 1& 0\\ 0& 1\\ \end{pmatrix}$$

то элементы матрицы S, при подстановки $a = \frac{1}{4}$имеют следующий вид:
$s_{11} = s_{22} = 1 + \sum\limits_{n =0}^{\infty}\frac{1}{2^n}$
$s_{12} = s_{21} = \sum\limits_{n =0}^{\infty}\frac{1}{2^n}$

Т.к. ряд $\sum\limits_{n =0}^{\infty}\frac{1}{2^n} = 2$, то матрица S принимает вид:
$S = \begin{pmatrix} 3& 2 \\ 2& 3 \\ \end{pmatrix}$

Но это не приводит к правильному ответу(

-- 18.02.2021, 16:08 --

Нет, общий вид всё таки такой:

$A^n = \begin{pmatrix} 2^{n-1}a^n&2^{n-1}a^n\\ 2^{n-1}a^n& 2^{n-1}a^n\\ \end{pmatrix}$

-- 18.02.2021, 16:17 --

И тогда элементы S, при$a = \frac{1}{4}$принимает вид:

$s_{11} = s_{22} =1 + \sum\limits_{n = 0}^{\infty}\frac{1}{2^{n+1}}$
$s_{12} = s_{21} =\sum\limits_{n = 0}^{\infty}\frac{1}{2^{n+1}}$

$S = \begin{pmatrix} 2 & 1\\ 1& 2\\ \end{pmatrix}$

-- 18.02.2021, 16:18 --

Что тоже неверно...

[ewert]

sirin0880 в сообщении #1505585 писал(а):

И тогда элементы S, при$a = \frac{1}{4}$принимает вид:

$s_{11} = s_{22} =1 + \sum\limits_{n = 0}^{\infty}\frac{1}{2^{n+1}}$

Не то начало суммирования.

[nnosipov]

sirin0880
Еще один способ вычислить $S$ --- вспомнить про школьную формулу суммы бесконечной геометрической прогрессии. (Это на тот случай, если захотите независимо проверить свой ответ.)

-- Чт фев 18, 2021 22:51:50 --

sirin0880 в сообщении #1505481 писал(а):

$$2^n*\frac{1}{4^n}$$

Типичная свертка Дирихле (the Dirichlet convolution).

[svv]

Последуем совету nnosipov и покажем, что если ряд сходится, то $(E-A)S=E$.

[sirin0880]

ewert в сообщении #1505605 писал(а):

Не то начало суммирования.

Если положить, что
$s_{11}=s{22}=\frac{1}{2}+\sum\limits_{n=0}^{\infty}\frac{1}{2^{n+1}}=1.5$
Для этих элементов матрицы S это верный ответ, но
$s_{12}=s{21}=\sum\limits_{n=0}^{\infty}\frac{1}{2^{n+1}}=1$ - не верно.
В ответе указано, что должна получится следующая матрица:
$S = \begin{pmatrix} 1.5& 0.5\\ 0.5&1.5\\ \end{pmatrix}$

Можете,пожалуйста, объяснить в чём подвох? И почему суммирование должно начинаться с $\frac{1}{2}$,если $A^0 = I$ - единичной матрице?

[svv]

sirin0880 в сообщении #1505645 писал(а):

И почему суммирование должно начинаться с $\frac{1}{2}$,если $A^0 = I$ - единичной матрице?

Не должно. Оставьте единицу перед суммой, как была. Дело не в ней. У Вас обе суммы ($\sum$) записаны неправильно. Не то начало суммирования, как выразился ewert.

Не смотрите сейчас на то, какой получается ответ, верный он или нет. Тем более, не подгоняйте формулы под ответ. Запишите правильно суммы.

[Pphantom]

Оффтопик отделен в «Звездочка как знак умножения»