Достаточно широко известна функция знака

.
Определив ее как

можно уменьшить количество индикаторов в выражении до двух. Можно ли обойтись совсем без индикаторов? Мне пришло в голову следующее решение:
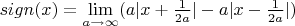
. Есть ли какие-то другие, возможно более известные или изящные варианты? Крайне желательно без использования дельта-функций и т.д., поскольку суть задачи как раз в том, чтобы обойтись максимально простыми средствами.