В трёхмерном пространстве дана стандартная спираль с единичным радиусом и постоянной кривизной, являющаяся кривой на цилиндрической поверхности.
Пусть она параметрически задаётся так:

, где

, то есть скорость движения в любой момент

равна 1. Тогда поверхность спиральной трубки, вычерчиваемой окружностью с центром, двигающимся по спирали и с плоскостью в любой момент перпендикулярной спирали, задаётся параметрически так:

где
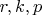
- положительные константы и

, при этом

- радиус этой трубчатой поверхности,

- координата на спиральной оси этой трубчатой поверхности (то есть длина фрагмента спирали от

до

), а

- угол, инвариантный относительно выбора

, под которым берётся точка на окружности-сечении этой трубчатой поверхности с центром в
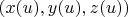
(под инвариантностью имею в виду инвариантность относительно выбора

спирали в декартовой системе координат с началом в точке
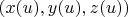
, осью

, направленной по вектору

и правильно подобранной ориентацией осей

и

).
Вопрос состоит в том, существует ли какая-та спиральная намотка на эту поверхность, получающаяся определением угла

, как дважды непрерывно дифференцируемой функции от

, такая, что у неё всюду постоянная кривизна?
Понятно, что если просто брать кривую на этой поверхности с углом-константой

, то мы получим некоторую стандартную спираль и у неё всюду будет постоянная кривизна, но этот вариант не является спиральной намоткой именно с той точки зрения, что угол не меняется, поэтому точно обозначу ограничение так:

, то есть инвариантный угол в любой момент

дважды непрерывно дифференцируемо растёт и растёт достаточно быстро, чтобы достигнуть любого значения.
p.s.
Под кривизной я подразумеваю стандартную кривизну пространственной кривой, задаваемую формулой
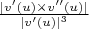
, где

Самый естественный вариант, когда

, где

, я уже проверил и в этом случае кривизна непостоянна.
К сожалению явная формула кривизны в моём случае - то ещё страшилище, что уж говорить о решении дифференциального уравнения

, где

- кривизна в точке

. Поэтому надежда в первую очередь на то, что посоветуете, как доказать, что такой спиральной намотки не существует, ибо как известно, утверждение о том, что кривизна и кручение постоянны накладывают очень сильные ограничения на кривую (она обязана быть стандартной спиралью), а значит и просто постоянность кривизны должна накладывать сильные ограничения. Возможно, тут надо как-то применить топологию, но моих знаний по-моему недостаточно.
Если же всё же такая спиральная намотка существует, то было бы очень интересно найти её явное выражение.