Дисперсия интеграла

[Ms-dos4]

Доброго времени суток. В процессе решения физической задачи появилась следующая проблема.

Пусть $\{ {\tau _k}\} $ - независимые случайные величины (континуальный случай), пока не будем характеризовать их распределение (котрое, однако, известно). Нам дана некоторая функция ${f(x,y)}$ (преимущественно рассматривается вид $f(x,y) = f(x + y)$), такая, что $\left| {f(x,y)} \right| < M$ на $\mathbb{R}^2$, также функция является быстроубывающей (быстрее любой степени) на хвостах. Для начала рассмотрим сумму

$${S_N} = \frac{1}{N}\sum\limits_{k = 1}^N {f(t,{\tau _k})} $$

Здесь всё понятно, легко находится математическое ожидание, дисперсия такой величины (в терминах моментов ${f(t,{\tau _k})}$). При больших $N$ применима классическая ЦПТ (ввиду ограниченности $f$). Однако больше интересует следующая величина

$${I_N} = \int\limits_{ - \infty }^{ + \infty } {S_N^2dt} $$

С вычислением математического ожидания проблем нет, а вот при вычислении дисперсии я утыкаюсь в величину $\operatorname{cov} [R({\tau _1} - {\tau _2}),R({\tau _1} - {\tau _3})]$ (остальные величины вычисляются в терминах моментов $R(x)$ - автокорреляционной функции для $f$), с которой неясно, что делать далее. Есть ли какие-то методы нахождения характеристик таких интегралов или придётся использовать разложения в ряды? Я бы очень хотел избежать таких оценок.

Второй пункт - распределение ${I_N}$. Казалось бы, классическая ЦПТ тут не применима (по отношению к интегральным суммам, так как слагаемые зависимы), тем не менее, как показывают численные результаты, для различных функций $f$ и распределений $\tau $ всё таки показывают сходимость к нормальному распределению, хоть и относительно медленную. Можно ли как-то это показать? Заранее спасибо за помощь.

P.S.Естественно, аналитическое нахождение распределения ${f(t,{\tau _k})}$ и затем N-кратные свёртки не рассматриваются.

[_hum_]

Насчет распределения. Я бы заметил, что
$I_n = \int_{\mathbb{R}}dt \Big(\int_{\mathbb{R}}f(t,u)dF^*_n(u)\Big)^2$,
где $F^*_n(u)$ - построенная по случайным величинам $\tau _1,...,\tau _n$ (и рассматриваемая как случайная функция) так называемая эмпирическая функция распределения.
А далее можно обратиться к так называемым функциональным предельным теоремам. Я такие встречал, например, в А.А. Боровков "Математическая статистика" (1997), Глава 1, параграф 6, теорема 3, а также параграф 8, теорема 2. Последнюю, вроде как вам было бы хорошо применить в случае, если подходящий функционал дифференцируем в указанном там смысле.
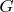
В вашем случае наверное, если функция $f$ - "хорошая", например, подходит под применение интегрирования по частям в интеграле Лебега-Стильтеса, стремится к нулю на бесконечностях, то можно было бы попробовать рассмотреть в качестве функционала $G $ функционал:
\begin{multline*}G(F) = \int_{\mathbb{R}}dt \Big(\int_{\mathbb{R}}f(t,u)dF(u)\Big)^2 = \\ \int_{\mathbb{R}}dt \Big( f(t,u)F(u)|_{-\infty}^{+\infty} - \int_{\mathbb{R}} F(u)f'_u(t,u)du \Big)^2 = \\ \int_{\mathbb{R}}dt \Big( \int_{\mathbb{R}} F(u)f'_u(t,u)du \Big)^2 \end{multline*}$
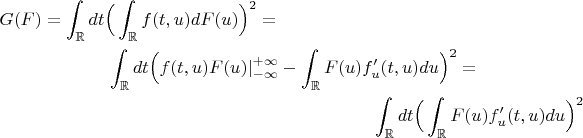
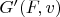
Ну, и тогда можно попытаться воспользоваться теоремой 2. Производная (в указанном в Боровкове смысле) этого функционала $G'(F,v)$ получится, если не ошибаюсь, наподобие:

$$G'(F,v) = 2\int_{\mathbb{R}}dt \Big( \int_{\mathbb{R}} F(u)f'_u(t,u)du\Big)\Big( \int_{\mathbb{R}} v(u)f'_u(t,u)du \Big).$$

(конечно, если там все подынтегральные предельные переходы возможны).
Ну, и останется только выяснить, какое распределение у случайной величины $ \int_{\mathbb{R}} w^0(u)f'_u(t,u)du$, где $w^0$ - Броуновский мост (Если, конечно, теорема в той формулировке, что есть, достаточна, а не требует еще каких-то замен переменных. Я сильно не вникал, но встречал по тексту мимолетные договоренности о таких заменах) Думаю, это довольно известная задача, и наверняка ее уже решали.

[Ms-dos4]

_hum_
Благодарю за ответ! Да, задача должна быть известна, но я найти не сумел (видимо не знаю где и как именно искать). Теперь по поводу Боровкова. Честно говоря, довольно трудно читать его изложение, но попробую описать то, что я понял.
Мы имеем функционал

$$G({F_N}) = \sum\limits_{k = 1}^N {f(t,{\tau _k})} = \int\limits_{ - \infty }^{ + \infty } {{{\left[ {\int\limits_L {f(t,\xi )d{F_N}(\xi )} } \right]}^2}dt} $$

Как я понял, их ${F_0}$ - это "предельная" функция распределения ${F_N}$ (буду писать её без нуля), то теорема 8 говорит, что

$$G({F_N}) - G(F) \to \frac{1}{{\sqrt N }}G'(F,B(F))$$

(где $B$ - Броуновский мост). Находим производную

$$G'(F,v) = 2\int\limits_{ - \infty }^{ + \infty } {\left[ {\int\limits_L {f(t,\xi )dv(\xi )} \int\limits_L {f(t,\xi )d{F_N}(\xi )} } \right]dt} $$

Тогда получаем, что

$$G({F_N}) - G(F) \to \frac{2}{{\sqrt N }}\int\limits_{ - \infty }^{ + \infty } {\left[ {\int\limits_L {f(t,\xi )dB(F)} \int\limits_L {f(t,\xi )dF(\xi )} } \right]dt} $$

Здесь

$$$\int\limits_L {f(t,\xi )dF(\xi )} = M[f](t)$$$

а первый интеграл

$$\int\limits_L {f(t,\xi )dB(F)} = \int\limits_L {\left[ {f(t,\xi ) - M[f](t)} \right]dW(F)} $$

имеет нормальное распределение с дисперсией

$${\sigma ^2} = \int\limits_L {{{\left[ {f(t,\xi ) - M[f](t)} \right]}^2}dF} $$

Но я пока всё ещё не понимаю, как это может помочь нам найти параметры и распределение $G(F)$, интеграл по времени никуда "не пропал".

[_hum_]

Ms-dos4 в сообщении #1468536 писал(а):

Как я понял, их ${F_0}$ - это "предельная" функция распределения ${F_N}$ (буду писать её без нуля)

Да. И она же известная вам функция распределения случайной величины $\tau_i$.

Ms-dos4 в сообщении #1468536 писал(а):

Находим производную

На всякий случай, будьте осторожны - судя по формулам, вы использовали исходную форму функционала и провели манипуляции формально. А ведь, например, интеграл по $d(F + v)$ может быть не определен.(Я специально изначально старался перевести все к виду функционала, в котором все промежуточные объекты существуют, чтобы таких вопросов не возникало).

Ms-dos4 в сообщении #1468536 писал(а):

Но я пока всё ещё не понимаю, как это может помочь нам найти параметры и распределение $G(F)$, интеграл по времени никуда "не пропал".

Если я правильно понимаю ваши обозначения (очень сложно читать, когда привык уже под греческими понимать случайные величины :) ), я бы поступил так. У вас есть выражения для $f $ и $F$. Соответственно, вы можете напрямую вычислить $M[f](t)$. Далее, считая, что можно менять порядок интегрирования, приходим к:

$$G({F_N}) - G(F) \to \frac{2}{{\sqrt N }} {\int\limits_L \left[ \int\limits_{ - \infty }^{ + \infty }{\left[ {f(t,\xi ) - M[f](t)} \right]M[f](t)dt \right]dW(F)} } $$

Это интеграл Ито (кстати, опять обращаю внимание, что вы его получили формально). Поскольку подынтегральная функция детерминированная, то напрашивается (наверняка, это какой-нибудь известный факт), что в этом случае распределение интеграла Ито нормальное (как вариант линейной комбинации нормальных). Матожидание и второй момент (а значит и дисперсию) наверняка можно вычислить, опираясь на свойства интеграла Ито. Напрашивается, что матожидание нулевое, а второй момент, с учетом Ito isometry, равен интегралу от квадрата соответствующей функции.

p.s. Кстати, почему вы пишете W(F), ведь зависимости W от нет?

[Ms-dos4]

_hum_
Изометрия Ито это то, что нужно, спасибо! Ну а пишу $dW(F(u))$, так как это вроде бы так и есть, если следовать выводу теоремы и дальнейшим примерам. Боровков просто обозначает $fg(x) = f(g(x))$ (если что, я использую издание 2010 года). Во всяком случае в такой постановке всё получается на ура.
P.S. По поводу некоторой формальности манипуляций - в данном случае вроде-бы всё хорошо, так как все объекты максимально "хорошие", да и у физиков всё не так "строго".
Ещё раз выражаю глубочайшую благодарность. Нужно будет заняться этим материалом.