Линейное преобразование

[fondet]

Условие задачи:
Вычислить матрицу линейного преобразования $\varphi $ множества векторов плоскости с заданным на ней базисом, если $\varphi$ есть проектирование плоскости на прямую $ x + y = 0 $ (1) параллельно прямой $ 4x + 5y = 0 $ (2)

Мои рассуждения:
1. Для начала выпишем определения: 1.1) Сумма подпространств - это линейная оболочка их объединения.
1.2)Сумма подпространств $U$ и $W$ называется прямой (обозначение $U \bigoplus W$), если любой вектор $v \in U + W$ имеет единственное представление вида $u + w$, $u \in U$,$w \in W$
1.3) Пусть $V = U \bigoplus W$. Тогда отображение $ P: v = u + w (u \in U, w \in W) \mapsto w$ называется проецированием $V$ на $W$ параллельно $U$
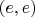
1.4) Матрица $A$ линейного преобразования $\varphi$ в паре базисов $(e,e)$ имеет следующий вид: в её $i$-ом столбце записаны координаты $\varphi(e_i)$ в базисе e. То есть на месте $(j,i)$ записана $j$-ая координата вектора $\varphi(e_i)$ в базисе $e$.


2. Обозначим $V$ - плоскость. $W$ - пространство всех векторов ($x_1,y_1$), для которых верно $ x_1 + y_1 = 0 $.
$U$ - пространство всех векторов ($x_2,y_2$), для которых верно $ 4x_2 + 5y_2 = 0 $.

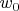
3. Замечаем, что любой вектор $v \in V$ представляется в виде $\lambda_1 \cdot u_o + \lambda_2 \cdot w_0$ (*), где $u_0$ и $w_0$ - базисные векторы $U$ и $W$ соответственно.
Это следует из условия задачи: нам говорят о проектировании плоскости $V$ на (1) параллельно (2) - а проектирование (по определению) возможно только в прямой сумме. Следовательно, плоскость $V$ представляет собой прямую сумму (1) и (2). Следовательно, $V$ - это множество всех возможных линейных комбинаций векторов из $U$ с векторами из $W$. А любой вектор $u \in U = \lambda_1 \cdot u_0 $. Аналогично любой вектор $w \in W = \lambda_2 \cdot w_0 $

4. Из (*) получаем, что $(u_o, w_o)$ - базис $V$ (линейная независимость очевидна, так как прямые (1) и (2) не параллельны).

5. $u_o = 1 \cdot u_0 + 0 \cdot w_0 \Rightarrow \varphi(u_0) \mapsto 0 = 0 \cdot u_o + 0 \cdot w_0$
$w_o = 0 \cdot u_0 + 1 \cdot w_0 \Rightarrow \varphi(w_0) \mapsto w_0 = 0 \cdot u_0 + 1 \cdot w_0$

6. Запишем матрицу линейного преобразования по определению:

$$\begin{equation*} A = \begin{pmatrix} 0 & 0\\ 0 & 1 \end{pmatrix} \end{equation*}$$

Понятно, что ответ неверный, так как я абсолютно нигде не учел вид уравнений (1) и (2). Но я не вижу, где в моих рассуждениях ошибка.
Правильный ответ:

$$\begin{equation*} A = \begin{pmatrix} -4 & -5\\ 4 & 5 \end{pmatrix} \end{equation*}$$

[mihaild]

Вы записали матрицу перехода в базисе $(u_o, w_o)$. И действительно, проецирование на прямую, натянутую на $w_o$, параллельно $u_o$, в этом базисе так и записывается.
Но обычно в таких задачах нужно записать матрицу в стандартном базисе - $(0, 1), (1, 0)$.

(Оффтоп)

Одновременное использование $o$ и $0$ в качестве индексов ИМХО крайне неудачная идея.

[fondet]

mihaild в сообщении #1452085 писал(а):

обычно в таких задачах нужно записать матрицу в стандартном базисе - $(0, 1), (1, 0)$.

Спасибо. Это действительно так. Перерешал задачу для стандартного базиса - ответ сошелся.

Тему можно закрывать