Является ли
Цитата:

тогда и только тогда, когда
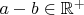
, где

- множество положительных действительных чисел
отношением порядка или нет? Если нет, то какой именно части определения "отношения порядка" оно не соответствует? Если да, то выполните ваше обещание.
Прям не знаю как мне быть... Вопрос-то выеденного яйца не стоит.
Но всё равно надо проконсультироваться у профессионала.
Вот вздымщик Цыпа писал(а):
Просто "следующего" самого по себе элемента увы, не бывает.
Бывает

. Постоянно встречается в

и не только.
А мне как то больше нравится традиционное название -
отношение непосредственного следования ...

Г-н
вздымщик! К вам вопрос на две копейки...

Известно, что запись бинарного отношения порядка иногда читают так: элемент
 следует за
следует за элементом

. Скажите, пожалуйста, надо ли дополнительно указывать кто за кем следует, или по умолчанию подразумевается, что в записи

элемент

всегда является следующим за

?
Вот г-н
MaximKat в своём определении некого отношения порядка на множ-ве

использовал знак "больше"

, что в данном конкретном случае не ведёт к путанице, но не указал какое число за каким следует, и теперь приходится нам гадать между двумя вариантами: то ли

, то ли

. Помогите разобраться, пожалуйста.
