Необходимо найти топологию на множестве

, порожденную семейством множеств

, если
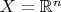
и

- множество всех замкнутых шаров.
Закрытый шар в метрическом пространстве

с радиусом

и центром

это множество точек
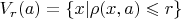
. Если мы говорим о множестве всех замкнутых шаров в

-мерном пространстве это все пространство? Как замкнутые шары могут образовать топологию? Это означает, что их пересечение и объединение должно давать тоже замкнутый шар. Это возможно, если это сфера в сфере с единым центром. Как это правильно записать? Ведь цетром

метрического пространства может быть любая его точка.