О проблеме Лежандра
Для решения этой проблемы необходимо знать закономерности образования разностей
между простыми числами. Более простой задачей является определение закономерностей
образования разностей между взаимно простыми вычетами ПСВ (приведенная система вычетов)
по модулю

, расположенными в порядке их возрастания.
Здесь мы имеем две закономерности образования разностей.
Первая очевидная закономерность ПСВ.
Разности

образуется с ростом

в начале и в конце ПСВ.
Условно будем считать такой рост линейным prime порядком.
Вторая неочевидная закономерность ПСВ.
Две разности

образуется в ПСВ(

) на границах стыков ПСВ(

).
Здесь так же имеем линейный prime порядок, но с коэффициентом 2.
Номер стыка таких разностей определяется решением системы сравнений.
(

) N + ! (mod p_r)= 0
(

) N - ! ( mod p_{r - 1}) = 0
В свое время Лежандр предположил, что разность между достаточно большими
соседними простыми числами выражается неравенством

Сразу напрашивается контрпример

, но он купируется
достаточно большими простыми числами.
Предлагаю гипотезу для интервала вычетов ПСВ по модулю

В интервале (

) вычетов ПСВ по модулю

максимальная разность между соседними числами равна

, т.е.

- порядковый номер вычета в интервале ПСВ.
Интервал (

) состоит из простых чисел, кроме вычетов

и

)
Эту гипотезу в таком виде можно доказать, используя закономерности
распределения вычетов ПСВ.
В определении ПСВ ничего не сказано о интервале вычетов (

).
Этот интервал образуется в ПСВ по модулю

, если вычеты расположить в порядке
их возрастания, причем окончательно он формируется только в ПСВ по модулю

.
Почему ?
В ПСВ по модулям

и

этот интервал выходит за пределы модуля.
В ПСВ по модулю

этот интервал занимает более половины модуля (

)
В этих примерах очевидно просматривается первая закономерность.
Разность

возрастает с ростом модуля и является максимальной
в данных интервалах.
Но ПСВ по модулю

это опровергает наличием разности

в интервале (

). В чем дело?
Оказывается, начинает проявлять себя другая закономерность образования
разностей между вычетами ПСВ, которая в ПСВ по модулям

и

совпадала с первой закономерностью. Это разности

.
В ПСВ(

) интервал (

) возвращается в нормальное состояние, т.е.
разность

является максимальной.
Прежде всего уточним понятие стыков ПСВ по модулю

.
Иначе модуль

, т.е. мы разбиваем модуль

на составляющие модули ниже порядком, в данном случае первого порядка.
Между ними образуются стыки. Номера стыков

обозначаем в порядке
их следования в ПСВ.
С увеличением модуля ПСВ разности

меняют свое положение
в пределах модуля.
Составим таблицу положений этих стыков при различных модулях.
Ближайшие к началу ПСВ разности, начиная с

d . . . . ПСВ . . . .стык, N стыка от начала ПСВ;(центр стыка)
6 . . . . .

. . . . .

10 . . . .

. . . . .

14 . . .

. . . . .

22 . . .

. . . . .

26 . . .

. . . .

34 . . .

. . . .

38 . . .

. . . .

46 . . .

. . . .

58 . . .

. . . .

62 . . .

. . . .

74 . . .

. . . .

82 . . .

. . . .

86 . . .

. . . .

94 . .

. . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Разность

образуется на стыке ПСВ

в ПСВ (

)
Это 4-ый стык

При

разностей

в этом интервале ПСВ не может быть,
т.к. в этом случае

Остается доказать, что разности, превышающие

, находятся
за пределом интервала

.
Элементарный перебор таких интервалов до достаточно больших значений

показывает, что это именно так. Поэтому все дальнейшие рассуждения
относятся к достаточно большим числам, например от

в ПСВ по модулю

, при этом стыком

является

, т.е.

.
Цепочки простых чисел это последовательность сравнимых вычетов по модулю
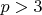
, составляющих данную разность. В ПСВ по модулю 6 эти вычеты следуют
в определенном порядке как вправо так и влево.

За центр цепочки можно принимать любые два вычета с разностью

Разности (от d = 28) образуются наложением цепочек простых чисел,
составляющих модуль ПСВ.
Полностью перекрыть разность цепочками простых не удается.
Оставшиеся места закрывают одиночные простые числа модуля.
Как крайний случай разности до

могут быть образованы
только одиночными простыми числами.
Чем больше цепочек имеет разность, тем меньше порядок ПСВ.
Особое место занимают разности типа

. которые могут иметь
максимальный состав одиночных простых чисел при минимуме цепочек.
Это разности

, т.е первые разности в ПСВ(p_r\#)
В качестве примера, разность

в ПСВ(

) имеет одну цепочку

и 8 одиночных простых чисел, тогда как в ПСВ(

) эта разность
имеет 4 цепочки (

) и 3 одиночных простых числа (

).
Вообще, разность

уникальна по составу
Простые числа цепочек образуют стык, относительно которого располагаются
разности в ПСВ, но часто этот стык не является полным праймориалом, т.е.
меньшие простые числа не имеют цепочек, но большие их имеют. В этом
случае такой стык будем записывать

, где

простые числа цепочек,
причем

. где

число свободных простых чисел,
образующих данную разность.
Ориентировочно можно считать

в пределах разностей

При дальнейшем увеличении

эта дробь несколько уменьшается.
Данные отношения

и

основаны на том, что цепочка из двух вычетов
с разностью

в разности

должна иметь зазор как минимум

т.е.

Одиночные простые числа определяют число этих разностей в ПСВ.
Зная состав разности по цепочкам и одиночным простым можно определить
место данной разности в ПСВ. В общем виде расположение разностей в ПСВ
определяется формулой

, где

- номер стыка,

- стык,

- сдвиг разности от оси стыка.
Для решения нашей гипотезы достаточно определить стык разности d в ПСВ, т.е.
определить

.
Несколько примеров из A048670 (

- число свободных

)
d , , , , ПСВ . . . .s . . . . . стык . . . . . . . . .N , , , . . . . . . . .K
40 . . . .

. . .3 . . . . .

. . . . . . . .677 . . . . . . . . . .2161
66 . . . .

. . .3 . . . . .

. . . . . . .39089. . . . . . . . 8903033
90 . . . .

. . .4 . . . .

. . . . . .2708158 . . . . . .6516941167 (здесь непоследовательный стык)
132 . . .

. . .4 . . . . .

. . . . . . 7840026 . . . . 208099059838039
200 . . .

. . .3 . . . . .

. . . . . . . .1 . . . . . .1522047068009676092181549507173.
282 . .

. . .2 . .

. . . . 1391401 . . . .2816010717078635988567530201271827
432 . .

. . .2 . . .

450 . .

. . .2 . . .

476 . .

. . .2 . . .

550 . .

. . .2 . . .

574 . .

. . .2 . . .

.
600 . .

. . .2 . . .

616 . .

. . .2 . . .

742 . .

. . .2 . . .

810 . ..

. . .2 . . .

867 . .

. . .2 . . .

1030. .

. . .2 . . .

1110. .

. . .3 . . .

Все это указывает на то, что мы имеем дело с третьей закономерностью образования разностей.
С ростом разности

растет и стык, к которому привязана эта разность, причем
этот рост несоизмерим по скорости роста разности

и стыка

. Более того, рост стыка
несоизмерим и с ростом

, что дает нам право утверждать, что разность

является максимально возможной в интервале

в ПСВ по модулю

Необходимо уточнить, что фактически разность

относится только к интервалу

, т.к. остальные вычеты всего интервала

имеют другие меньшие разности.
Чтобы полностью представить распределение максимальных разностей, надо разделить
весь интервал

на отдельные участки по границам квадратов простых чисел.
В каждом из них будет своя максимальная разность.
Эта разность в принципе должна изменятся для каждой пары соседних простых чисел..
Интервал

ограничен числами

и

, которые входят в состав интервала не являясь
простыми числами, но являются вычетами данной ПСВ. Принимаем

, тогда

т.к.


В интервале

все вычеты, кроме

простые числа.
Обозначим

, тогда

или

, но

. следовательно
