Munin, благодарю, но я другого не понимаю: группа определена на пространстве размерности 2, а матрица три на три.
Группа в некотором смысле "самостоятельна" по отношению к пространству. (Строже говоря, мы можем рассматривать множество изоморфных групп, но на смысловом уровне всё это одна и та же группа - действующая на разных множествах, или не действующая вообще, записываемая иногда в разных обозначениях.)
Если нам надо рассмотреть движения евклидова пространства

то мы можем сделать так: рассмотрим линейное пространство

и в нём плоскость

Эта плоскость, очевидно, двумерное вещественное пространство. Тогда каждое движение этого двумерного пространства может быть сопоставлено какому-то линейному преобразованию

(понимаете как?), и это гомоморфизм групп. А линейные преобразования

записываются в виде матриц

Движения двумерного пространства - сохраняют длины (расстояния, метрику) на двумерном пространстве. Что сохраняют соответствующие преобразования

? Не длину, нет. Поэтому не стоит накладывать на них такое требование.
По крайней мере, эти линейные преобразования должны оставлять плоскость

на месте.
Кроме того, если точка
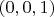
остаётся на месте, то тогда движения есть только повороты и отражения вокруг этой точки, и
тогда линейные преобразования сохраняют длины в

Но это только подгруппа группы движений.
В общем, вот так вот, постепенно, разбираетесь со смыслом блоков матрицы
 -- 06.06.2019 19:06:50 --
-- 06.06.2019 19:06:50 --Подскажите, пожалуйста, что имелось в виду в абстракте?
Это не абстракт, а вступление. Абстракт там одна строчка :-)
Хорошо, если объект обсуждения всё-таки просто вспомогательная конструкция, а не именно матричная реализация, то почему в публикации там равенство стоит, в определении?
Это общепринятая реализация, так что почему бы для удобства и не написать равенство?
Кстати, эта реализация дальше по тексту вообще нигде не используется.