так, предлагаю два решения: одно неполное (до определённого момента) в декартовой системе координат, другое (полное) в полярной системе координат.
1.
введём двухмерную прямоугольную декартову систему координат

, плоскость которой совпадает с плоскостью движения точки, начало координат - с центром осциллятора и

,

- вектора начального положения и скорости заданные в этой системе координат.
Тогда, решая дифференциальное уравнение

по обеим осям, приходим к тому, что
1.1

1.2

отсюда предполагая, что орбита точки - это всё-таки эллипс найдём его размеры и моменты времени, когда расстояния от точки до центра осциллятора достигают наибольшего и наименьшего отдаления: для этого решим решим уравнение





таким образом имеем нужные моменты времени, подставляем их в

и получаем, что если ввести переменные
1.3

1.4

,
то

и уравнение

преобразуется в

таким образом если мы считаем, что форма орбиты - это эллипс или окружность или отрезок или точка, то форму каждого из этих геометрических объектов полностью задают два числа, что можно доказать.
1.5

1.6

таким образом если

, то орбита - эллипс, если

- окружность, если

- отрезок и, наконец, если
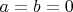
- точка (последние три объекта рассматривать не будем)
Всюду далее будем считать, что

, попробуем в декартовой системе координат доказать, что орбита - эллипс. Мне пришли в голову только три варианта:
1а) найти координаты точки в момент наибольшего (или наименьшего) отдаления
1б) по этим координатам найти угол

между лучом из центра в данную точку и какой-то из двух осей координат
1в) далее повернуть всю траекторию точки на данный угол в нужном направлении, воспользовавшись формулой ротации


1г) проверить, что получившаяся траектория - действительно эллипс (в этом случае знать размеры и форму эллипса в принципе не нужно)
2а) с помощью ввода параметра угла

и формулы ротации составить уравнение (непараметрическое, то есть без времени) эллипса необходимой формы, повёрнутого на данный угол

2б) найти данный угол

, сопоставив это уравнение с параметрическим (от времени) описанием траектории.
2в) доказать, что этот угол действительно подходит, подставив координаты от времени вместо переменных в уравнении эллипса из пункта 2а)
3а) то же, что 2а)
3б) перевести систему уравнений 1.1,1.2 в одно уравнение, избавившись от параметра времени
3в) сопоставить это уравнение с уравнением эллипса повёрнутого на угол

и найти угол

3г) проверить, что угол действительно подходит.
Немного о каждом из способов:
первый способ уже на шаге 1.1 доставляет огромные неприятности связанные с тем, что синус и косинус половины арктангенса некой переменной выражаются через эту переменную очень большой формулой, которая к тому же зависит от того в каком диапазоне находится данная переменная. С каждым шагом этот способ доставляет новые неприятности, которые, если не упростить максимально всё на предыдущем шаге оборачиваются на порядок большими проблемами.
второй способ более привлекателен,
однако в декартовой системе координат ротация громоздка и поэтому на шаге 2.3 при подстановке получается очень большая формула, а на шаге 2.2 формула угла также довольно большая.
третий способ в декартовой системе координат также слишком громоздок.
Поэтому я перешёл в полярную систему координат, в которой, например, третий способ гораздо более компактен.
Не привожу данные рассуждения в виде формул, так как они гораздо более габаритные, чем всё, что было перед этим.
Приведу решение в полярной системе координат третьим способом:
2.

(на первом месте угол, на втором модуль вектора)

2.1

2.2

следовательно:












уравнение нужного, повёрнутого на угол

, эллипса выглядит в полярной системе координат, как

приравниваем это уравнение эллипса к уравнению из 2.6 и, подставляя вместо

и

ноль, получаем, что

отсюда

проверяя подстановкой убеждаемся, что

угол

, заданный такими синусом и косинусом действительно существует и удовлетворяет нужным свойствам. Отсюда орбита - действительно эллипс. Если решать в декартовой прямоугольной - всё куда хуже.
И всё же, неужели нельзя сделать как-нибудь проще, без таких больших формул?