Чтобы не мучиться:
Значительно упростил доказательство.
Формулировка: если

, где

и

, то

имеют общий простой делитель.
Доказательство:
Допустим, что контрпример существует и

взаимно просты, т.е. два числа из трёх нечётные и третье чётное. Не теряя общности, можно говорить о том, что

нечётное, в противном случае просто перенесём одно из нечётных слагаемых в другую часть и сменим знак. Итак, контрпример имеет вид

и при делении на

образуются две несократимые рациональные дроби.

Пусть

несократимая рациональная дробь, тогда её разложение на три куба выглядит так:
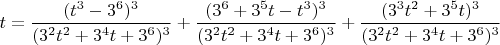
проверяется это
непосредственноПодставляя

вместо

имеем:



Таким образом, разложив контрпример на сумму кубов, приведя к общему знаменателю и заменив

, имеем:

Нетрудно заметить, что

числа нечётные при любых

и, так как

нечётно по определению, то в левой части уравнения находится число нечётное, в то время как в правой части суммы

и

есть числа нечётные, а сумма

есть число чётное.
В итоге в левой части у нас число нечётное, а в правой чётное. Противоречие. Следовательно одно из нечётных чисел должно быть равно нолю.
Так как

нолю равняться не может (доказательство просто - выделить полный куб), следовательно нолю должно равняться либо

либо

, что невозможно при взаимно простых

.
Следовательно наше допущение ложно и контрпримера не существует.