Я просто имел ввиду, что не всегда в учебниках по физике объясняют математические темы, которые там используются так, что мне это легко понять.
С такой формулировкой совершенно согласен, с ней не поспорить.
Разумеется, есть хорошие учебники и средние учебники (не говоря уже о плохих). Кроме этого, с точки зрения математики, учебники физики могут или хорошо вводить математику, или средне, или вообще никак. Давать тут общие для всех оценки - бессмысленно.
И помимо этого, главное качество учебника по физике - быть учебником
по физике. Есть учебники, заслуженно любимые и ценимые именно за изложение физики, и придирки к изложению математики в этих учебниках - как минимум, второстепенны. Цикл
Ландау-Лифшица ("тома
Ландау") скорей относится к этой разновидности.
----------------
В общем, я бы посоветовал не учиться по одному учебнику, а заглядывать в разные, сравнивать и выбирать, что вам больше нравится и подходит. С другой стороны, не стоит слепо бросаться следовать советам типа "не учитесь этому по учебнику физики, читайте учебник по математике". Зависит от ваших целей. Вас для физики вполне могут устраивать пониженная строгость и доказательность, зато для вас преимуществом будут краткость, и сосредоточенность на технике и вычислениях. Увы, самые рекомендуемые для математиков учебники - обладают недостатками с точки зрения физиков.
А геометрический смысл этих величин знать не нужно?
Думаю, нужно. Хотел бы узнать. Пока ответить о таком смысле не могу.
Ну вот суньте нос в
Анго, это быстро.
А те вещи (например теорема Гаусса и т. д.), которые я не читал где-то ещё, мне естественно в ЛЛ-2 понять трудно.
Ой, кошмар-кошмар-кошмар.
Теорему Гаусса к этому моменту читатель должен был увидеть уже много раз в разных местах. В курсе матанализа ("Анализ-2", анализ векторных полей). В курсе общей физики (как теорему для электрического и магнитного поля). В курсе ураматов / ДУЧП - как теорему, выполняющуюся и применяемую для решения уравнений Лапласа и Пуассона.
Ландау-Лифшиц рассчитывают на всё это предварительное знакомство.
Если вы не прошли предварительно курсов матана, линала и общей физики - вам читать
ЛЛ просто рано. Извините. Вы забегаете вперёд. (Ну и получаете закономерные последствия этого.)
В принципе, это можно, но надо быть готовым к тому, что полного понимания не будет, полноценного знания не будет, это всё предварительный наскок, и надо будет потом в своё время заново всё перечитывать и переосознавать. Это можно делать самопально при наличии интереса, времени и сил, для поддержки и развития мотивации, но не как часть полноценного процесса обучения.
Если же вы дошли до чтения
ЛЛ-2 по стандартной программе, имея такие пробелы в базе, вам надо их срочно заполнять. И в любом случае, не могу дать вам оптимистичных прогнозов, такая ситуация - это
катастрофа, на её исправление потребуются годы, и хорошо, если вы всё-таки этим исправлением будете заниматься, до получения диплома, и после.
Мне всё-таки кажется, что чтобы понять (мне лично, конечно) математику (некоторую) в физике, нужно или читать раннее об этом где-то в книге по математике (т. е. в книгах по физике зачастую объясняют "новую" математику, просто бывает непросто понять некоторые факты без доказательства или без того, как к этому пришли и т. д.)
Это всё бывает сильно по-разному. Зависит от конкретного предмета. Вообще в среднем и в целом - да, желательно сначала математику, потом физику. Но есть некоторые отдельные темы (их не более порядка 20 %), которые в книгах по физике объясняются даже лучше, нагляднее, чем в книгах по математике. Например, для векторного поля очень полезен такой наглядный образ, как "линии поля", а они в книгах по математике или не вводятся вообще, или сильно потом и как что-то сложное и факультативное. Но на одном образе "на пальцах" далеко не уедешь, а расчёты векторных полей учат делать именно учебники математики.
Второго мне иногда не хватает и приходится искать объяснения более основательные и где начинают с каких-то простых вещей типа записи

, где это потом все расписывают, обозначают

, обозначают

и получают

.
1) Стандартные курсы линала, конец курса - главы про тензоры.
2)
Анго, или что-то ещё в таком духе. У меня нет подборки хороших книг на эту тему, я в детстве ещё
Маделунга читал, но не стану рекомендовать.
В ЛЛ-2 сказано, что антисимметричному 4-тензору 3-го ранга можно поставить в соответствие дуальный ему 4-вектор.
Попробуйте расписать это по компонентам. Очень полезно.
(Это частный случай такого факта: в

-мерном пространстве с метрическим тензором, можно антисимметричному тензору ранга

поставить в соответствие дуальный ему вектор. Потренируйтесь ещё на

)
Действительно, получается так, что если

- антисимметричный по каждой паре индексов, и

то етому можно соотнести уравнение

. Они оба дадут, что все 4 компоненты

равны нулю. Я так понимаю, такое соотношение справедливо тогда, когда антисимметричный тензор равен нулю, да?
Да, но это нулевой случай. Интереснее ненулевой.
Понятно, что если

, то здесь нельзя соотнести этому уравнение для

т. к. не хватает одного индекса.
Нет, это и есть готовое уравнение для

а величины

считаются известными (4 числа). Здесь 4 уравнения, и
если мы знаем, что

полностью антисимметричный, то это условие даёт нам ещё 60 уравнений, и всего получится 64 уравнения, задающих 64 элемента тензора (из них 40 нулевых, и остальные 24 образованы всего четырьмя числами со знаками

).
И ещё, если мы захотим обобщить это соответствие на другие размерности и ранги тензоров, то нам нужно учитывать эти два числа, как я понял. Т. е. интересно, как обобщать это соответствие между антисимметричными и дуальными тензорами. Т. е. можно ли взяв полностью (это обязательно, да?) антисимметричный тензор любой размерности и любого ранга соотнести ему дуальный тензор?
Общая схема такая:
полностью антисимметричный тензор ранга

дуален полностью антисимметричному же тензору ранга

где

- размерность пространства. Это ещё называют "
дуальность Ходжа" или "
звёздочка Ходжа" (Hodge star) по обозначению звёздочкой (в
ЛЛ-2 в верхнем индексе, а в нотации
внешних форм - перед формой = тензором).
Эта конструкция позволяет обобщить школьные операторы градиента-ротора-дивергенции на пространства любой размерности. Если мы вместо вектора

рассмотрим ковектор (вектор с ковариантным индексом) = 1-
форму 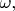
то получим
где оператор

(называющийся
внешний дифференциал) - единообразный оператор дифференцирования антисимметричных тензоров любого ранга:
- сначала берут тензорную производную ("простую"), повышая ранг на 1;
- а потом в полученном результате выделяют чисто антисимметричную часть.
-- 01.12.2018 15:11:32 --Чисто из любопытства: а Вы как предпочитаете, делить на

, или нет?
Зависит от открытой передо мной книгой, в соответствии с которой я делаю выкладки. Обычно, наверное, не делить. Потому что в физике принято

без "пополама".
Хорошее замечание.
misha.physicsПривыкайте, что в некоторых выкладках есть так называемые "соглашения" (о знаках, сигнатурах, коэффициентах, базисах, ещё кое-чём), которые могут быть в разных книгах разные. Обычно они оговорены где-то в начале книги, и потом вся книга написана в указанном сеттинге. Довольно часто бывают расхождения между книгами по физике и по математике. Бывают расхождения между советскими-российскими книгами и американскими-англоязычными. В клинических случаях даже между "московской школой" и "ленинградской-питерской школой". Это может поначалу сбивать, если пытаться выкладки из одной книги применять к другой книге, или пытаться работать с несколькими книгами сразу. Потом возникает привычка, и можно формулы конвертировать даже "на лету", в уме. Уважаемый
пианист напомнил о двух видах антисимметризации:
![$$F_{[\mu\nu]}=F_{\mu\nu}-F_{\nu\mu}\qquad ?\qquad F_{[\mu\nu]}=\tfrac{1}{2}(F_{\mu\nu}-F_{\nu\mu}),$$ $$F_{[\mu\nu]}=F_{\mu\nu}-F_{\nu\mu}\qquad ?\qquad F_{[\mu\nu]}=\tfrac{1}{2}(F_{\mu\nu}-F_{\nu\mu}),$$](https://dxdy-04.korotkov.co.uk/f/7/8/8/7883f2e76e6c5939b7d97fc277347e1a82.png)
второй способ удобнее тем, что если тензор и так антисимметричен, то антисимметризация его никак не меняет. (Для антисимметризации по

индексам возникает, соответственно, множитель

)
Ещё один важный момент того же рода: во времена написания
ЛЛ-2 вполне нормально было написать книгу, в которой
 - латинские индексы - 4-мерные, а
- латинские индексы - 4-мерные, а
 - греческие индексы - 3-мерные.
- греческие индексы - 3-мерные.
"Боролись" две традиции, и на сегодня одна из них победила с большим преимуществом, и на сегодня везде принято:
 - греческие индексы - 4-мерные (причём часто именно "мю-ню");
- греческие индексы - 4-мерные (причём часто именно "мю-ню");
 - латинские индексы - 3-мерные.
- латинские индексы - 3-мерные.
Это может сбивать с толку, если сравнивать формулы
ЛЛ-2 с другими книгами или с Wikipedia.
Другая деталь: система единиц.
ЛЛ-2 написан в системе СГС Гаусса - наиболее популярной среди физиков-теоретиков (хотя соглашение

сегодня также крайне популярное, в
ЛЛ-2 не используется). В Wikipedia сдуру все формулы переписаны в СИ, а в учебниках такое хоть и бывает, но сравнительно редко. В совсем продвинутых книгах - от КТП и дальше в теорию струн - иногда предпочитают систему СГС Хевисайда, которая отличается от СГС Гаусса другим расположением в формулах множителей типа

Хевисайд, в отличие от Гаусса, логичнее обобщается на другие размерности пространства-времени.