В одной теме, попавшей в карантин, было предложено рассмотреть выражение

.
Любопытно, что данное выражение преобразуется с использованием элементарного тождества

которое труднее придумать, чем доказать. Да, разумеется, оператор

симметрический,
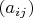
-- его матрица, по повторяющимся суммирование.
А что для несимметрических операторов в трехмерном евклидовом пространстве?
(Оффтоп)
кстати, почему не двухмерное и тримерное?