Как я понял, не всегда целесообразно доказывать непрерывность функции на ограниченном промежутке непосредственно через определение непрерывности. В книге Основы матанализа Ильина и Позняка видел доказательство для линейной функции

на основе определения предела того, что

. А это и есть доказательство её непрерывности на всей области определения. То же видел и для постоянной функции

. Далее, на основе теорем умножения и сложения непрерывных функций можно доказать непрерывность остальных функций, например, степенной

. В моём примере
![$y = 1 - \sqrt[3]{x^2}$ $y = 1 - \sqrt[3]{x^2}$](https://dxdy-01.korotkov.co.uk/f/c/7/d/c7dfd2df84b91d588813689b549132f482.png)
функция, исходя из этих теорем, будет непрерывна на всей своей области определения, а значит и будет непрерывна на отрезке
![$[-1, 1]$ $[-1, 1]$](https://dxdy-01.korotkov.co.uk/f/4/3/c/43ca5ad9e1f094a31392f860ef481e5c82.png)
.
Но с доказательством непосредственно через определение "

" непрерывности не совсем понял.
Есть ряд теорем о непрерывности суммы непрерывных функций, сложной функции и так далее. Но можно доказать и "по определению в терминах эпсилон-дельта". Просто берём точку

, принадлежащую промежутку, и разбираемся с ней через соответствующий предел. И обобщаем на все точки....
Т.е., можно взять любую точку, например,
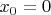
и вычислять для неё предел? А далее обобщить на все точки промежутка?