Реально достигнутый уровень значимости (

-value) - это совсем не есть вероятность ошибки первого рода.
Вероятность ошибки первого рода - это вероятность при верной

её отвергнуть. Это - характеристика критерия. Она никак не зависит от тестируемой выборки. Она есть уже потому, что есть критерий.
Например, при проверке гипотезы

по выборке объёмом

из распределения Бернулли критерием с критической областью

вероятность ошибки 1-го рода есть вероятность


-value равно вероятности получить по абстрактной выборке, отвечающей

, худшее согласие с

, чем получено по данной выборке. Или, иначе, это наибольшая из вероятностей ошибок первого рода всех тех критериев, которые по данной числовой выборке будут принимать

. И характеризует он, в отличие от вероятности ошибки первого рода, не столько критерий, сколько данную числовую выборку и степень её согласия с проверяемой гипотезой.
Чтобы в примере выше найти

-value, надо взять конкретную числовую выборку. Например, пусть для неё

. Тогда

-value будет

Если увеличивать критическую область у критерия, заменяя

на меньшие значения, или - равносильно - увеличивать ошибку первого рода, то пока эта ошибка не дорастёт до

(или граница с

не уменьшится до
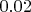
), критерий по данной числовой выборке будет принимать

.
Так что с Вашей трактовкой реально достигнутого уровня значимости я согласна во всём, кроме последнего предложения
Таким образом, вероятность несправедливости утверждения "гипотеза H2 верна" меньше p-value.
Чтобы говорить о вероятности того, что гипотеза верна, нужно иметь эксперимент, в котором "гипотеза H_1 верна" и "гипотеза H_2 верна" являются событиями, имеющими вероятности. Это совсем иная байесовская постановка вопроса (отчего у меня дежавю?). Просто если шансы по типичной выборке из

получить худшее согласие с

, чем получено по проверяемой числовой выборке, очень малы, то согласие последней с

очень плохое и гипотезу по ней отвергают.
С учетом этого мне становится наконец-таки понятным, почему в одних источниках хорошим считается большой уровень значимости (типа, "больше 0.05"), а в других - наоборот, чем меньше, тем лучше (меньше 0.05).
Естественно: если Вы проверяете гипотезу, которую хотите принять, то "хорошо" для этих целей иметь большое значение

-value. Если же основная гипотеза - нежелательна (кормили-кормили пациентов лекарствами, а средние у этой и контрольной выборок одинаковы), то Ваша надежда - её отвергнуть, и тогда хорошим значением

-value для Вас будет число, меньшее

.