Практическая суть уровня значимости

[--mS--]

_hum_ в сообщении #1315539 писал(а):

Не могли бы Вы начать с простого - например, с двух простых - $H_1$ = "монетка c $p=1/2$" и $H_2$ = "монетка c $p=3/4$" в предположении, что эти гипотезы равновероятны, и показать, в чем ошибочность моих рассуждений?

Вам про сложные альтернативы говорят, а Вы снова простую предлагаете. Если Вы будете рассматривать состоятельный критерий, то формула Байеса, конечно, верна, и Ваша (асимптотическая) формула тоже.

-- Пн май 28, 2018 19:11:33 --

_hum_ в сообщении #1315539 писал(а):

что, кроме того, что про нее написано в Боровкове, мне еще нужно знать?

Достаточно и Боровкова. Например, параграфы из 3-й главы: 45-й (особенно п.4), а также 46-й.

[_hum_]

--mS-- в сообщении #1315540 писал(а):

Вам про сложные альтернативы говорят, а Вы снова простую предлагаете. Если Вы будете рассматривать состоятельный критерий, то формула Байеса, конечно, верна, и Ваша (асимптотическая) формула тоже.

Ага. Значит, если простые гипотезы, то такая суть использования уровня значимости проходит, и дело лишь в том, что это не срабатывает для сложных гипотез.
Если так, то хорошо - становится яснее.

После просмотра Боровкова. Насколько я понял, основная проблема применения подхода - это то, что для сложных гипотез в формуле

$$P(H_2 | A_\varepsilon) = 1 - \dfrac{\varepsilon }{\varepsilon + \frac{P(H_2)}{P(H_1)}P(A_\varepsilon |H_2)} $$

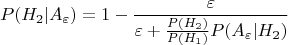
величина $P(A_\varepsilon |H_2)$ в общем случае при любом фиксированном $n$ может быть сколь угодно мала. И, насколько я понимаю, это следствие того, что семейства распределений гипотез могут быть "неразделяемы" (распределение из семейства для одной гипотезы может сколько угодно мало отличаться от распределения из семейства для другой). Это так?
Если да, то есть еще такое соображение: на практике, если брать пример с той же монеткой, вроде бы не имеет смысла рассматривать "неразделенные гипотезы". То есть, достаточно проверять $H_1 =$ "монетка с $p=1/2$" и $H_2 =$ "монетка c $p \not\in (1/2-\Delta, 1/2 +\Delta)$", для некоторого выбранного $\Delta > 0$ (определяемого из соображений существенности различий для задачи исследования, например, точности измерений). В этой постановке, вроде бы, уже удается добиться за счет выбора большого $n$, чтобы $P(A_\varepsilon |H_2)$ было сколь угодно близким к единице, и тем самым вернуть содержательность первоначальной трактовки.

[--mS--]

Разумеется, в этом частном случае это сработает.

(Оффтоп)

Дальнейшего смысла своего участия в этой теме не вижу.

[_hum_]

--mS--
Ясно, спасибо. А подскажите, по каким ключевым словам искать разработку подобного подхода (например, какие разделения возможны, и как от них зависит скорость приближения $P(A_\varepsilon |H_2)$ к единице)?

[Евгений Машеров]

Проблема только в одном:

(Оффтоп)

либо трусы, либо крестик

либо "уровень значимости", либо "вероятности гипотез". Это разные парадигмы.
Когда мы говорим в терминах "уровня значимости", мы ничего о вероятностях гипотез не предполагаем. Это специальный подход, позволяющий не рассматривать эти вероятности. Поскольку вывода о значениях этих вероятностей вне байесовского подхода сделать невозможно, а байесовский подход инструмент мощный и полезный, позволяющий инкорпорировать данные об априорных вероятностях, но если у нас их нет - заменять на произвольно выбранные это мошенничество. Поэтому p, хоть и "вероятность" - но не "вероятность гипотезы". Это вероятность получить то, что мы видим, если справедлива нулевая гипотеза.