Записал кучу уравнений, ответ отличается только множителем

. Не понимаю почему.
Потенциальная энергия в зависимости от угла

имеет вид:
![$$\[E = \frac{{kqQ}}{{4{R^2}{{\cos }^2}\varphi }} + 2mgR{\cos ^2}\varphi \]$$ $$\[E = \frac{{kqQ}}{{4{R^2}{{\cos }^2}\varphi }} + 2mgR{\cos ^2}\varphi \]$$](https://dxdy-04.korotkov.co.uk/f/7/2/d/72db6c4999c2a709f6c0dcc5f5aaa8f382.png)
Делаем замену
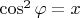
и исследуем функцию
![$$\[E(x) = \frac{{kqQ}}{{4{R^2}x}} + 2mgRx\]$$ $$\[E(x) = \frac{{kqQ}}{{4{R^2}x}} + 2mgRx\]$$](https://dxdy-03.korotkov.co.uk/f/a/7/6/a76a3faa1a395fa9e09f6f17780cd2f482.png)
Запишем уравнение
![$\[E'(x) = 0\]$ $\[E'(x) = 0\]$](https://dxdy-02.korotkov.co.uk/f/1/9/6/196348b21e195dace5326c47174e8ba182.png)
:
![$$\[ - \frac{{kqQ}}{{4{R^2}{x^2}}} + 2mgR = 0\]$$ $$\[ - \frac{{kqQ}}{{4{R^2}{x^2}}} + 2mgR = 0\]$$](https://dxdy-02.korotkov.co.uk/f/5/3/a/53aaab73c8e9d2ed1f5c4c44c50096ad82.png)
и получим
![$$\[x = \frac{{\sqrt 2 \sqrt {mgRkqQ} }}{{4mg{R^2}}}\]$$ $$\[x = \frac{{\sqrt 2 \sqrt {mgRkqQ} }}{{4mg{R^2}}}\]$$](https://dxdy-02.korotkov.co.uk/f/1/f/9/1f91600fc57dba20d14d1f6143cca46582.png)
Заметим, что
![$$\[E''(x) = \frac{{kqQ}}{{2{R^2}{x^3}}}\]$$ $$\[E''(x) = \frac{{kqQ}}{{2{R^2}{x^3}}}\]$$](https://dxdy-01.korotkov.co.uk/f/8/7/9/8792d00ebcea5ee3060e46ed18a36a2a82.png)
и если полученный корень подставить во вторую производную, то она будет положительна, значит это минимум. Подставляя полученный минимум в

, получим:
![$$\[{E_{\min }} = \frac{{k\;q\;Q\;\sqrt 2 mg}}{{\sqrt {mgRk\;q\;Q} }}\]$$ $$\[{E_{\min }} = \frac{{k\;q\;Q\;\sqrt 2 mg}}{{\sqrt {mgRk\;q\;Q} }}\]$$](https://dxdy-01.korotkov.co.uk/f/c/f/b/cfbb9fae5a1294d1b6f37c4d41eb447282.png)
По условию, это выражение функция

приминает в верхней точки полости, но в этой точке

, откуда получим уравнение

:
![$$\[{k\frac{{qQ}}{{4{R^2}}} + mg2R = \frac{{k\;q\;Q\;\sqrt 2 mg}}{{\sqrt {mgRk\;q\;Q} }}}\]$$ $$\[{k\frac{{qQ}}{{4{R^2}}} + mg2R = \frac{{k\;q\;Q\;\sqrt 2 mg}}{{\sqrt {mgRk\;q\;Q} }}}\]$$](https://dxdy-04.korotkov.co.uk/f/7/1/5/7154754f314d0cc1e8d0fbb16813af9582.png)
отсюда
![$$\[{q = \frac{{8{R^3}gm}}{{Qk}}}\]$$ $$\[{q = \frac{{8{R^3}gm}}{{Qk}}}\]$$](https://dxdy-04.korotkov.co.uk/f/7/9/d/79dad6b83cf439d06bb3f4d643a30ee282.png) -- 24.05.2018, 15:02 --
-- 24.05.2018, 15:02 --Вообще, как-то громоздко задача решается.
Тут на 6 странице решение короче.