Найти ортогональный базис для подпространства

[CruelShadow]

Здравствуйте. Проверьте, пожалуйста, в правильном ли направлении я двигаюсь в решении этой задачи.

Условие: на векторном пространстве R^{4} задано скалярное произведение, матрица Грама которого по отношению к стандартному базису имеет вид

\begin{pmatrix} 7 & 7 & 2 & 0 \\ 7 & 10 & -3 & -5 \\ 2 & -3 & 10 & 7 \\ 0 & -5 & 7 & 10 \end{pmatrix}

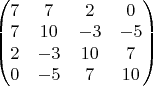
Найти ортогональный базис для подпространства, порожденного векторами

\begin{pmatrix} 3 \\ 3 \\ -1 \\ 3 \end{pmatrix}, \begin{pmatrix} 3 \\ 1 \\ 1 \\ 2 \end{pmatrix}, \begin{pmatrix} 0 \\ -2 \\ 2 \\ -1 \end{pmatrix}, \begin{pmatrix} 2 \\ -1 \\ -3 \\ -2 \end{pmatrix}.

Решение: обозначим данные вектора как u_{1}, u_{2}, u_{3}, u_{4}, а искомый ортонормированный базис как e_{1}, e_{2}, e_{3}, e_{4}. Воспользуемся процессом ортогонализации Грама-Шмидта:

e_{1} = u_{1} = \begin{pmatrix} 3 \\ 3 \\ -1 \\ 3 \end{pmatrix}.
e_{2} = u_{2} - \frac{ \left( u_{2}, e_{1} \right) }{ \left( e_{1}, e_{1} \right) } \cdot e_{1} = u_{2} - \frac{ 7 }{ 7 } \cdot u_{1} = u_{2} - u_{1} = \begin{pmatrix} 0 \\ -2 \\ 2 \\ -1 \end{pmatrix}. 7 в числителе взял как пересечение 2-го столбца и 1-й строки в матрице Грама.
e_{3} = u_{3} - \frac{ \left( u_{2}, e_{1} \right) }{ \left( e_{1}, e_{1} \right) } \cdot e_{1} - \frac{ \left( u_{3}, e_{2} \right) }{ \left( e_{2}, e_{2} \right) } \cdot e_{2} = \ldots.

[Brukvalub]

Распишите подробнее, как вы вычисляете скалярное произведение двух векторов.

[CruelShadow]

Brukvalub в сообщении #1296842 писал(а):

Распишите подробнее, как вы вычисляете скалярное произведение двух векторов.

Я думал, что скалярное произведение мы просто берём из матрицы Грама. Однако, кажется, я ошибся. Для нахождения скалярного произведения нужно сложить сумму попарных произведений координат?

[Brukvalub]

Нет.

[CruelShadow]

Brukvalub в сообщении #1296863 писал(а):

Нет.

Не подскажите тогда, пожалуйста, как именно?

[Brukvalub]

Не подскажу. Порекомендую ознакомиться с определением матрицы Грама.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.