Пожалуйста, при наборе формулы окружайте её двумя знаками доллара, внутри формулы долларов быть не должно. Иначе вид формулы искажается, и разобраться труднее. Например,

у Вас выглядят как векторы, хотя это, скорее всего, комплексные числа. Символ
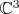
(если Вы именно его имели в виду) кодируется
\mathbb C^3.