Есть вот какой функциональный ряд

.
Где

и

.
Нужно чтобы он сходился и получившуюся функцию можно было дифференцировать по обоим переменным. Значит нужна некоторая равномерная сходимость по обоим переменным. Как поступать в этом случаи. В теории

можно оценить через

Но что делать с

? Пока удалось показать, что

, где

многочлен степени не большей чем
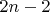
.