Здравствуйте, уважаемые участники. Такая задача:
Цитата:
Вычислите радиус сходимости ряда Тейлора (в окрестности точки

) для функции

Используйте выражение вида

Преобразую в

Затем беру известный ряд

, соответственно, для него

.
Соединяем,

соответственно,

, Но! для

.
Я не нашел, что такое "радиус сходимости в окрестности точки" (возможно, плохо искал), есть только термин "центр круга сходимости". Вижу два варианта ответа:
забить на  , тогда
, тогда  .
.
принять за центр круга  , тогда
, тогда 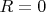 (или пустое множество (?)).
(или пустое множество (?)).
В обоих случаях ничего нет, напоминающего корень.
Намекните, куда двигаться дальше? Спасибо!