Я устал, я не ухожу (с) почти Ельцин

Пардон, что долго молчал, но сейчас отчётный период и нет возможности сосредоточиться на математике кроме некоторых выходных. Да и трудно даётся решение вопросов не о смысле, а о форме его подачи (формализация), но это необходимо, конечно. Поэтому, чтобы не тянуть – изложу сейчас то, что готово.
Формулирую, что такое

– в деталях:



Тут

– это алгоритм-решение, который должен был бы представлять данный язык в классе

.

– это алгоритм проверки, который представляет данный язык в классе

.

и

– время работы соответствующих алгоритмов.
При этом:

- это я не «доигрался» до логики 2-го порядка, а это условное сокращение для записи вида

где алгоритм

– это «универсальный алгоритм», который исполняет программный код из первого аргумента, передавая ему в качестве аргументов всё, начиная со 2-го аргумента в

.
впрочем и последняя формула – тоже сокращение для:

.
Где

– это «условная компиляция», которая проверяет, действительно ли в

программный код в нужном формате или нечто ошибочное.
Как побочный эффект моего исследования вопроса – был найден способ свести вопрос о

к второй части детального представления этого

. А именно – Если будет доказана вторая часть

:


то будет доказано и

. А

построены так, что заведомо известно, что для корректного

верно:

Последнее позволяет не рассматривать 1-ю часть детального представления для

. При этом эти

вовсе не какие-то заведомо недоказуемые утверждения, а как раз заведомо доказуемые при результате алгоритма-проверки

, и вопрос только в размере доказательства.
Точнее: верно

, а иначе будет выполнена 1-я часть детального представления (так построено утверждение

):

Вернемся теперь от побочной линии к основной.
Перепишем детальное представление для

в новом виде:



.
Мы добавили к слову часть

– это ничего не меняет в принципе (просто разбили слово на 2 части, где новая часть ничего не несет, кроме возможности увеличить размер допустимых для рассмотрения сертификатов). Ещё мы обозначили здесь переменной

«опровергающее утверждение» вместо обозначения

– так как это обозначение потребуется нам в дальнейшем для специального случая и будет обозначать некоторые конкретные «сконструированные» утверждение. Но ещё мы включили явную зависимость алгоритма проверки от того алгоритма-решения, к которому эта проверка относится:
У нас появилась часть

– содержащая программный код. Для одних слов она – сертификат, а для других – часть слова. И тоже, вроде, ничего принципиального – мы можем взять любой язык из класса

с «классическим» алгоритмом проверки и добавить в этот алгоритм такую часть

, от которой ничего не зависит, кроме требования, чтобы к размеру сертификата (при расчете ограничений) добавлялся ещё и её размер. Но мы этим не ограничимся, разумеется, и рассмотрим язык не с таким слегка изменённым «квазиклассическим» алгоритмом проверки.
Ещё один нюанс – полиномы

и

могут в некоторых случаях иметь степень ноль при аргументе
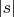
, если соответствующее им слово не будет зависеть от размера
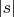
, но это будет разбираться отдельно далее. Не принципиален для дальнейшего рассмотрения вопрос о зависимости

ещё и от

: Мы будем рассматривать такие

, размер которых больше размера

. Поэтому ограничение в любом случае оказывается в пределах

.
Напоминаю, что

в логике – это аналог подстановки, так как

.
При этом обозначение

я использую в качестве сокращения для более правильного (но в котором больше скобок) обозначения:

.
В свете последнего детального представления для

отмечу, что спецификой в реализации языка

является вот что: Часть данных, соответствующих программному коду алгоритма-решения

, является частью одного слова и частью сертификата для другого слова. И при этом те слова вида:

которые алгоритм

может подтвердить, как принадлежащие языку

, полностью соответствуют наличию подтверждающих сертификатов вида

, где

И, таким образом, возможность алгоритма-решения

подтвердить принадлежность языку

слова

имеется лишь тогда, когда «расширенное слово»

или слово

принадлежит языку

.
Это «расширенное» слово отличается от слова, про которое алгоритм-решение должен дать ответ. Таким образом, удалось разделить 2 функции, которые исполняет одно и то же слово в «классическом» языке из

по 2-м разным словам.
Думаю, уже достаточно написано формул, чтобы их обсуждать. Но дам картину в целом (не формально), какие формулы последуют далее, и что я доказываю в итоге (для справки, а не для обсуждения – пока нижесказанное не формализовано).
Далее я ввожу в рассмотрение специфическое утверждение

, взятое (его идея) из теоремы о неопределимости математической логики. И это такое утверждение, которое алгоритм-решение

не может доказать в принципе. Более того, от способа и времени получения алгоритмом

ответа (который в корректном случае может быть только

), будет зависеть размер слова

, и, возможно, его принадлежность языку

.
Поэтому ограничение для времени поиска ответа для данного конкретного случая уже не может быть

– от размера искомого слова: нельзя ставить время работы в зависимость от того, что само зависит от времени его работы.
К тому же, возможности алгоритма-решения

описываются НЕ искомым им словом, а соответствующим ему «расширенным» словом. Ведь нам удалось разделить 2 функции, которое исполняет слово в «классическом» случае на 2 разных слова, как уже упоминалось.
Поэтому в детальном представлении для

появится зависимость от времени работы алгоритма проверки для специфического случая и «расширенного» слова. И это будет

, а соответствующее ему ограничение для алгоритма решения будет

. Кстати, для специфического случая мы будем иметь зависимость от слова, «которого нет» в языке

и судить о его размере можно лишь по времени работы алгоритма проверки. Вот на это время и будет опираться

.
Да, в пункте 6 потребуется поменять условие

на

чтобы добиться зависимости размера слова от времени работы алгоритма-решения. Сам

остаётся тем же и сохраняет все свои свойства и в уточненном варианте – насколько я поверхностно проверил.
После этого будет доказано, что с такими раскладами при результате

у алгоритма

за время

неизбежно (при достаточно больших по размеру

) появится доказательство у утверждения

(за счёт того, что размер доказательства зависит в основном от

, которое не участвует в ограничивающем полиноме для времени работы).
И вот здесь ранее я останавливал своё доказательство. Я думал, что для устранения возможности появления доказательства для

при результате

от алгоритма

потребуется неполиномиально больше времени на решение, чем требуется времени на проверку того, какой результат (

) будет в качестве этого решения. И это доказывало как раз задачу-первоисточник для

– что для любого алгоритма-решения есть такие задачи, проверка решения которых на равенство правильному ответу неполиномиально проще (быстрее), чем поиск этого ответа данным алгоритмом-решением.
Но теперь я думаю, что имеется доказательство и для


Просто всё детальное представление для

строится из предположения о том, какие смыслы у

и

должны быть у корректного алгоритма-решения. Но в специфическом случае для быстрого ответа смысл выводится логически. И смысл у

для алгоритма

для специфического случая при быстром возврате им результата может быть только один – «доказательство есть» )))) Потому что логика выше условных договорённостей.
Но раз условные договоренности являются частью детального представления для

и корректный алгоритм-решение обязательно должен их нарушить – то он уже не будет соответствовать «стандартным» требованиям к алгоритму-решению из класса

. А раз это произвольный алгоритм-решение – то нет ничего «стандартного» и при этом корректного среди алгоритмов, которые делали бы рассматриваемый язык языком класса

в «стандартном» понимании.
Но сказанное в последней паре абзацев имеет отношение к той будущей дискуссии, которая лишь предстоит (после оставшейся формализации) и которая не затрагивает то, что я хотел доказать изначально (и доказываю, как мне кажется).
Но не могу удержаться от нескольких абзацев «в топку» будущей дискуссии о том, что важнее – условные договоренности или логика.
Пример из жизни. Тебя спрашивают:
«Ты можешь спрогнозировать ответ, который даст на твои слова человек-наоборот?». Понятно, что если ты скажешь «Могу», то человек-наоборот ответит «Не могу», а если ты скажешь «Не могу», то ответом тебе будет «Могу».
Из «алгоритма проверки» ты знаешь, что ты – именно ты – не можешь дать правильный ответ на поставленный вопрос. И вопрос адресуется именно тебе. Поэтому ты сообщаешь «Не могу», потому что именно такой ответ сообщает о твоей неспособности в соответствии со сведениями от «алгоритма проверки». И этот же ответ заведомо означает, что человек-наоборот ответит «Могу». И ты дал правильное сообщение (прогноз), потому что стандартное «соглашение о кодировании» твоего сообщения-прогноза не работает в данном случае в отношении «человека-наоборот».
Но «соглашение о кодировании» сообщения-результата в данном случае и не требуется, потому что правильный формат сообщения в данном случае логически выводится из информации о твоих собственных возможностях (точнее, неспособностях) в соответствии с тем форматом, который принят для проверки твоих возможностей (неспособностей). Притом информация о твоих возможностях получается быстро в данном случае.
И да – мы выходим на формализацию понятия рефлексии, когда алгоритму для правильного ответа надо понимать, что вопрос задан именно ему. Это – гораздо принципиальнее и интереснее, чем даже вопрос про

, потому что открывается возможность для математической формализации принятия решений «живыми» разумными системами, которая невозможна без рефлексии. То, что мы делаем по 100 раз на дню, выделяя и решая задачи, которые стоят именно перед нами. И то, что до сих пор никаким «боком» не было формализовано в математике.