Получается, что при измерении импульса и координаты в состоянии, описываемом волновой функцией

, вероятность получить собственные значения

и

, равна 1
Как же так, разве можно при измерении импульса и координаты получить определенные значения этих физических величин?
так как разложение не должно менять свойства исходной волновой функции, то по идее,

должна оставаться собственной функцией оператора импульса
Не наводите тень на плетень :)
В вопросе идёт речь об обычном разложении в ряд Фурье (да, импульсное и координатное представления связаны преобразованием Фурье, разложение в ряд будет иметь место для частицы в ограниченной области, когда набор собственных функций дискретный, а так это преобразование Фурье). В общем случае - разложение по полной системе функций. Здесь нет ничего загадочного и ничто при таком разложении не теряется (равенство математически строгое, если система функций полная).
При этом тот объект, который Вы обозначаете

, является произведением скалярного коэффициента (скалярного произведения

) на

- собственную функцию оператора координаты (или
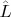
, как тут выше стали писать). C какой стати он должен оказаться ещё и собственной функцией оператора импульса, не коммутирующего с
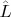
? Если настаиваете на своём - докажите :).
т.е.

и есть собственная функция

Ерунду пишете. Как я отметил выше,

- это скалярное произведение функций, комплексное число. Называть его функцией в данном контексте язык не поворачивается. :)) (Доп. Тут я, пожалуй, перегнул палку. Всё-таки функция, но другим переменным, по отношению к оператору - скаляр.
svv в сообщении #1237776 писал(а):
Вы используете систему таких функций, которые являются собственными сразу для двух операторов, и эта система полная. А существует ли она?
в том то и дело, что данную систему использует автор темы
Докажите. Продемонстрируйте публике, что функции

и

обе являются собственными функциями и оператора импульса, и оператора координаты.
Другое дело, что для свободной частицы в неограниченном пространстве речь должна идти о непрерывном спектре и о преобразовании Фурье, а не разложении в ряд.
т.е. идет речь о произведении двух операторов, причем именно двух некоммутативных операторов
Речь идет о разложении функции по полной системе других функций. При чём тут произведение операторов и их коммутатор?
Ну и ещё раз: если функция является суммой двух собственных функций какого-то оператора, то она, очевидно, тоже будет собственной функцией этого же оператора. Обратное, вообще говоря, не верно. Собственная функция оператора может быть представлена линейной комбинацией функций, не являющихся собственными. Это показывают примитивные прямые выкладки.
-- 02.08.2017, 22:29 -- Мне показалось, что функции

— это мои

Мне показалось, что

