Задача про белые и зеленые шары.

[Thinker]

Здравствуйте! Помогите, пожалуйста, решить задачу по теории вероятностей.

В мешке 78 белых и 2 зеленых шара. Из мешка наудачу вытягивают 2 шара и, не глядя, выкидывают, после чего в мешок докладывают 2 зеленых шара. Описанную процедуру повторяют $n$ раз. Какова вероятность того, что на $n+1$-й раз оба вытянутых шара будут белыми? Один белый и один зеленый?

Мне не приходит в голову ничего более остроумного, чем последовательно вычислять вероятности. Но, возможно, существуют какие-то более простые способы.

P.S. Я - не школьник и не студент, эта задача родилась из практики. Буду очень признателен всем, кто отзовется. Спасибо заранее.

[provincialka]

А прямой подсчет, что, сложный? Или вы из любви к искусству спрашиваете?

[Thinker]

Для меня сложен. Я вообще не очень силен в теории вероятностей и боюсь, что мое решение будет неверным.

[provincialka]

А вам как надо решить? Численно (программой) или формулой?
Можно рассматривать весь процесс как марковский, матрица перехода $A$ имеет размер $79\times 79$ и трехдиагональна. Умножая на нее исходные вероятности $(1, 0, ..., 0)$ мы получим вероятности 78, 77, ... , 0 белых шаров в урне.

То есть вектор вероятностей есть первый столбец мaтрицы $A^n$.

Есть ли этого ответа краткий вариант? Не знаю.

[Thinker]

Меня устроит и численное решение. А в том, что Вы написали про матрицы, я, к сожалению, не ориентируюсь.

[mihaild]

Попробуйте написать, что и как вы собираетесь считать, а там посмотрим.
Что именно вы хотите в ответе? Конкретную формулу для $n$? Не получится, скорее всего.

[provincialka]

mihaild, ТС вроде уже согласился на численное решение?

Thinker в общем, смотрите. Рассмотрим шаг $n, n = 0, 1, ...$. Число белых шаров к этому моменту может оказаться равным $78, 77, ..., 0$. На самом деле на первх шагах $0, 1,..$ белых шаров быть не может, но мы просто будем считать, что вероятность этого равна 0. Итак, на шаге $n$ вероятность иметь в урне мешке $k$ белых шаров равна $p_k^n$. Что будет происходить на следующем шаге? Если белых шаров было $k$, то их может стать $k, k-1$ или $k-2$, обозначим это число через $l$.
Надо посчитать (условные) вероятности этих вариантов, при условии, что изначально было $k$ белых шаров.

Так. Дпавайте я остановлюсь, скажите, что вы поняли и можете ли эти вероятности посчитать.

[mihaild]

provincialka в сообщении #1221139 писал(а):

ТС вроде уже согласился на численное решение?

Не очень понятно, что такое численное решение, зависящее от $n$.

И я бы предложил для начала рассмотреть задачу скажем для $4$ шаров, чтобы можно было выписывать все числа явно.
Вот изначально у нас было $2$ белых и $2$ зеленых шара. Мы вынули $2$ шара. С какой вероятностью что осталось в урне?

[provincialka]

mihaild
Ну, ясно, что не для произвольного $n$. Я тут по ходу написала на Excel подсчет для 10 шаров (8 белых). "Размножением" формул можно получить сколько угодно шагов... Ну, сколько Excel позволит

[Thinker]

provincialka в сообщении #1221139 писал(а):

На самом деле на первх шагах $0, 1,..$ белых шаров быть не может

Что это значит? Как так не может??

[provincialka]

А откуда им взяться? Если вначале было 78 белых шаров, вы вынули 2. Даже если они оба белые, в мешке еще осталось не менее 76 белых.

[Thinker]

Ой, да, я неверно Вас понял. Я думал, что $0, 1,...$ - это значения $n$

-- 01.06.2017, 22:20 --

mihaild в сообщении #1221141 писал(а):

Не очень понятно, что такое численное решение, зависящее от $n$.

Это решение может быть в виде таблицы, в которой, скажем, для первых ста $n$ приведены вероятности вынуть 2 белых шара или 2 разноцветных.

-- 01.06.2017, 22:24 --

mihaild в сообщении #1221141 писал(а):

И я бы предложил для начала рассмотреть задачу скажем для $4$ шаров, чтобы можно было выписывать все числа явно.
Вот изначально у нас было $2$ белых и $2$ зеленых шара. Мы вынули $2$ шара. С какой вероятностью что осталось в урне?

Если я правильно понимаю, с вероятностью $1/3$ осталось $2$ белых шара, $1/3$ - $2$ зеленых и $1/3$ - $2$ разноцветных.

[provincialka]

Thinker в сообщении #1221241 писал(а):

Если я правильно понимаю, с вероятностью $1/3$ осталось $2$ белых шара, $1/3$ - $2$ зеленых и $1/3$ - $2$ разноцветных.

Упс... мда, про марковскую цепь -- это я зря

Вот у нас 2 белых шара и 2 черных зеленых (кстати, почему -- зелёных??) Как можно вынуть один белый и один зеленый шар?
1. Первый -- белый, осталось 3 шара, потом -- зеленый
или
2. Первый -- зеленый, осталось три шара, потом -- белый.

Ну, или два белых: один белый (из 4 шаров) и снова белый (из оставшихся трех)

[Thinker]

provincialka в сообщении #1221276 писал(а):

Thinker в сообщении #1221241 писал(а):

Если я правильно понимаю, с вероятностью $1/3$ осталось $2$ белых шара, $1/3$ - $2$ зеленых и $1/3$ - $2$ разноцветных.

Упс... мда, про марковскую цепь -- это я зря

Вот у нас 2 белых шара и 2 черных зеленых (кстати, почему -- зелёных??) Как можно вынуть один белый и один зеленый шар?
1. Первый -- белый, осталось 3 шара, потом -- зеленый
или
2. Первый -- зеленый, осталось три шара, потом -- белый.

Ну, или два белых: один белый (из 4 шаров) и снова белый (из оставшихся трех)

Я же говорил, что слабоват в теории вероятностей. Те есть, правильно: с вероятностью $1/6$ осталось $2$ белых шара, $1/6$ - $2$ зеленых и $2/3$ - $2$ разноцветных?

-- 02.06.2017, 12:18 --

Шары зеленые, потому что задача рождена из практики.Там есть белые и зеленые объекты. (А черных нету )

[provincialka]

Thinker
Теперь верно! Видите, можете же!

Давайте пойдем дальше. Обозначим для общности $80 = N$ После $n$ шагов у нас может остаться от $0$ до $N-2$ белых шаров. Но каждый вариант ($k$ белых) имеет некую вероятность $p_k^n$. Зная эти вероятности, мы уже можем вычислить и нужные вам.

Вернемся в "нанозадаче", предложенной mihaild
Тут $k$ принимает значения $2, 1, 0$, при $n=0$ реализован только случай $k=2$, то есть вероятности $(p_2^0,p_1^0,p_0^0)$ имеют вид $(1,0, 0)$. На следующем шаге вероятности, как вы вычислили, будут равны $(p_2^1,p_1^1,p_0^1)=(1/6,2/3, 1/6)$
Что дальше? Предположим, мы нашли значения $(p_2^m,p_1^m,p_0^m)$, как посчитать $(p_2^{m+1},p_1^{m+1},p_0^{m+1})$?
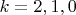
Число $k$ белых шаров может получиться, если перед этим их было $l=k, k+1, k+2$. Причем мы можем посчитать вероятность получения $k$ шаров при каждом $l$. Примеро так, как вы это сделали для $k = 2, 1,0$ при $l=2$. Обозначим эти вероятности пока $a_k^l$.

Как теперь найти $p_k^{m+1}$? По формуле полной вероятности, то есть разобрав все случаи.

$$p_k^{m+1} = a_k^kp_k^m+a_k^{k+1}p_{k+1}^m+a_k^{k+2}p_{k+2}^m$$

Так. Пока остановлюсь. Понятно ли это? Можете ли вы найти $a_k^l$ для $N=4$, $k,l$ от $0$ до $2$?

И еще вопрос: как у вас дела с матрицами? Знаете, как их умножают?