Упражнение из Кострикина-Манина

[Muvv]

Пусть с линейным отображением $g: L \to M$ конечномерных пространств связана цепочка отображений, построенных (см.ниже). Построить канонические изоморфизмы:
$ \operatorname{Ker} g^* \to \operatorname{Coker} g $, $ \operatorname{Coim} g^* \to \operatorname{Im} g $, $ \operatorname{Im} g^* \to \operatorname{Coim} g $, $ \operatorname{Coker} g^* \to \operatorname{Ker} g $.

Имеется цепочка отображений, разбивающая $g$ на части,
$\operatorname{Ker} g \to L \to \operatorname{Coim} g \to \operatorname{Im} g \to M \to \operatorname{Coker} g$.

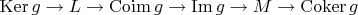
Попыталась построить, для упрощения задачи, канонический изоморфизм $ \operatorname{Coim} g^* \to \operatorname{Im} g $ в случае $\dim \operatorname{Ker} g = \dim \operatorname{Ker} g^* = 0$. Тогда легко строятся изоморфизмы $M^* \to \operatorname{Coim} g^*$, $M\to\operatorname{Im}g$. Т. е. 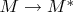задача построения изоморфизма $ \operatorname{Coim} g^* \to \operatorname{Im} g$ сводится к построению изморфизма $M \to M^*$, который является каноническим для заданного отображения $g$. Но как строить дальше, я не знаю.

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы не оформлены $\TeX$ом

Muvv
Наберите все формулы и термы $\TeX$ом.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.