Доброго всем времени суток. Уважаемые, помогите разобраться. На примере задачи: В покоящуюся тележку с песком общей массой

попадает пуля массой

, летящая со скоростью

и застревает в песке, после чего тележка начинает двигаться со скоростью

. Найти энергию, которая перешла в тепло? (Задачу взял из головы, может что и не так).
Из ЗСИ:

,
из ЗСЭ:

, откуда:

.
Возникли, наверное, дурацкие вопросы:
1) если правильно понимаю, при
неупругом ударе потери на тепло будут всегда? А как это объясняется в терминах физики?
2) если рассматриваем
абсолютно упругий удар двух бильярдных шаров, то потребовав отсутствия потерь
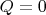
, из системы:

получу решение либо:

, либо:

, т.е. движущийся шар после удара остановится, а другой начнет движение со скоростью первого шара.
Верно ли отсюда сделать вывод, что если после соударения движутся оба шара, значит не обошлось без потери энергии в тепло? Как можно объяснить в терминах физики связь потери энергии и движение обоих шаров?