Вот это я не могу прочитать чисто синтаксически
Сейчас отвечу на более "глобальный" вопрос, может будет понятней. Ок?
Я, честно говоря, так и не понял, что все эти Ваши алгоритмы делают. Напишите формально, какой язык

и какое отношение

будут у Вашей "нехорошей" задачи?
В предлагаемом языке «слову» соответствует теорема

, предельный размер доказательства для неё в 2-х представлениях

и

, и аргумент долга (текст некоторого алгоритма-решения)

. Слово считается подтвержденным (существует «сертификат»), если длина строки

равна числу

, имеется доказательство

размером до

, и если теорема не равна утверждению

- это утверждение построено так, что алгоритм

заведомо не может найти «сертификат» для него.
Скорость работы алгоритма проверки разная для разных случаев. Если имеет место

, то полиномиальное ограничение на время работы

– что неполиномиально меньше чем у «общего»

, чей ограничивающий полином –

. Так как

неполиномиально меньше, чем
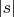
.
Вы понимаете, что у нас есть 2 (Два) полиномиальных ограничения на время работы? Для задачи в целом он больше (дольше), а для подзадачи

– он неполиномиально меньше. Меньшее может входить в большее, поэтому подзадача соответствует «общей» задаче и её полиномиальному ограничению, но для корректного «Эдипа» при решении вопроса о

«существует» такая задача из класса

, которая неполиномиально быстрее «общей». И не выдать соответствующий быстрый ответ – значит, быть неспособным свести эту подзадачу из класса

к классу

.
А выдать быстро – значит, утратить соответствие (равенство результатов) между решаемой тобой задачей, соответствующей аргументу долга

и такой же задачей, но в которой иной лишь аргумент долга – равный

.
Я строю задачу, в которой любые алгоритмы-решения могут решать только «свои» задачи – потому что алгоритм-решение соответствует некоторой части «слова» разбираемого «языка». Но существенным (с иным результатом и/или ограничением на время работы проверки) этот нюанс становится лишь на утверждениях типа

.
То есть – возврат 0 «Эдипом» при поиске сертификата для

– соответствует «языку». Хоть «Эдип» ищет доказательство для «слова» с теоремой

и аргументом долга
«объективно»,
но его работа соответствует аргументу долга
«Эдип с аргументом долга «объективно»».
Потому что дело не в том, для какого аргумента долга он ищет, а в том, «кто» ищет. Аргумент долга «Сфинкса» (то есть элемент слова в предлагаемом «языке») должен соответствовать фактам а не аргументу долга внутри «Эдипа».Так как: «Но словам ведь соответствуют понятия» (c) «Фауст». А частью «слова» у нас является алгоритм-решение с тем, что у него подставлено в качестве аргумента долга, а не то, что у него подставлено – независимо от самого алгоритма-решения.