Задача 2. Поперек шоссе лежит бревно массой

и длиной

. Чтобы освободить дорогу, его пытаются перетащить на траву, прикладывая силу вдоль бревна. Бревно перетащили наполовину длины.
![$\[{\mu _1},{\mu _2}\]$ $\[{\mu _1},{\mu _2}\]$](https://dxdy-04.korotkov.co.uk/f/7/c/0/7c0cb9424c481d6a110e267f31c14d4682.png)
- коэффициенты трения об асфальт и траву соответственно. Какая работа была совершена?
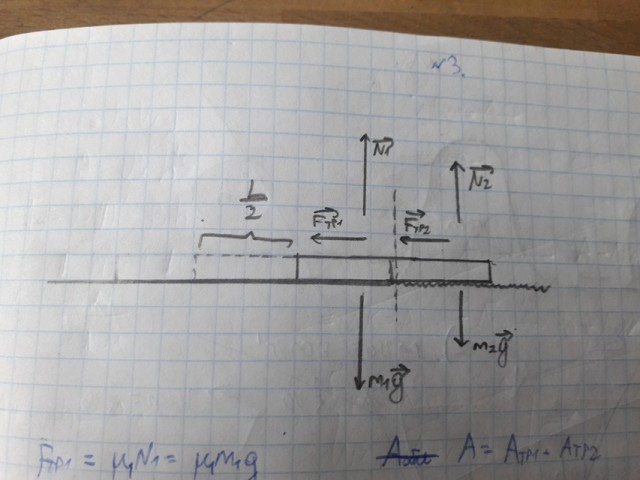
Решение.
Аналогично, как и в прошлой задаче, силы трения не постоянны, но можно найти их работы, считая площади под графиком:
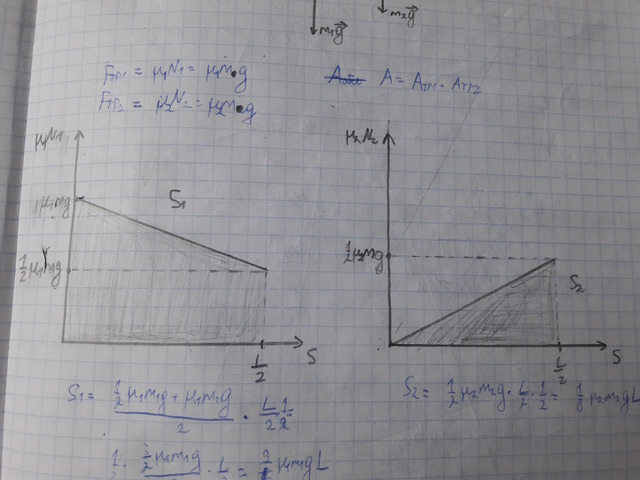
![$$\[{A_{{F_1}}} = \left| {{S_1}} \right| = \frac{{\frac{1}{2}{\mu _1}mg + {\mu _1}mg}}{2} \cdot \frac{1}{2} \cdot \frac{L}{2} = \frac{9}{{16}}{\mu _1}mgL\]$$ $$\[{A_{{F_1}}} = \left| {{S_1}} \right| = \frac{{\frac{1}{2}{\mu _1}mg + {\mu _1}mg}}{2} \cdot \frac{1}{2} \cdot \frac{L}{2} = \frac{9}{{16}}{\mu _1}mgL\]$$](https://dxdy-01.korotkov.co.uk/f/c/a/2/ca2c1a8939f4127dba0395696021b2a782.png)
![$$\[{A_{{F_2}}} = \left| {{S_2}} \right| = \frac{1}{2}{\mu _2}mg \cdot \frac{1}{2} \cdot \frac{L}{2} = \frac{1}{8}{\mu _2}mgL\]$$ $$\[{A_{{F_2}}} = \left| {{S_2}} \right| = \frac{1}{2}{\mu _2}mg \cdot \frac{1}{2} \cdot \frac{L}{2} = \frac{1}{8}{\mu _2}mgL\]$$](https://dxdy-01.korotkov.co.uk/f/c/a/8/ca842327105a9ffbb47fceabffc6459d82.png)
Вся работа

равна:
![$$\[A = {A_{{F_1}}} + {A_{{F_2}}} = \frac{9}{{16}}{\mu _1}mgL + \frac{1}{8}{\mu _2}mgL = \frac{{11}}{{16}}mgL({\mu _1} + {\mu _2})\]$$ $$\[A = {A_{{F_1}}} + {A_{{F_2}}} = \frac{9}{{16}}{\mu _1}mgL + \frac{1}{8}{\mu _2}mgL = \frac{{11}}{{16}}mgL({\mu _1} + {\mu _2})\]$$](https://dxdy-03.korotkov.co.uk/f/e/1/4/e1435e29bb1ce6f575398337abce236282.png) -- 19.02.2017, 16:51 --
-- 19.02.2017, 16:51 --Результат вообще говоря должен быть меньше, так как если полностью передвинуть бревно, то
ответ будет
![$\[\frac{1}{2}mgL({\mu _1} + {\mu _2})\]$ $\[\frac{1}{2}mgL({\mu _1} + {\mu _2})\]$](https://dxdy-04.korotkov.co.uk/f/b/a/b/babe3ec9a6752d0cb03f3c00e2a98ca182.png)