разбираться как советую я
Как советуете вы:
Пусть у нас есть фундаментальная последовательность вещественных чисел, т.е. классов ФПРЧ.
Да, например простая последовательность

тоже подойдет.
Ис каждого класса выбираем одну ФПРЧ.
Проще говоря, к каждому числу из списка

приписываем рациональную последовательность, которая сходится к этому числу. Практически это осуществить несложно. Для

это может быть последовательность

, для
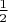
это

, и так далее...
Из первой последовательности берем первый элемент, из второй - второй и т.д.
В результате этого процесса получается

, то есть изначальная наша последовательность

.
На основании фундаментальности исходных последовательностей доказываем, что полученная тоже фундаментальна, т.е. определяет какое-то вещественное число.
В этом примере можно не сомневаться. Поскольку получилось так, что она совпала с

, которая изначально фундаментальна.
Оно-то и будет искомым пределом.
Мы не ищем предел. Вы не объяснили переход от фундаментальности к сходимости.