Может быть, в Вашем распоряжении есть и исходные линейные уравнения? (полученные из законов Кирхгофа) Давайте их.

Хорошо. Тогда я развернуто изложу условие задачи, стоящей передо мной.
Схема электрической цепи:
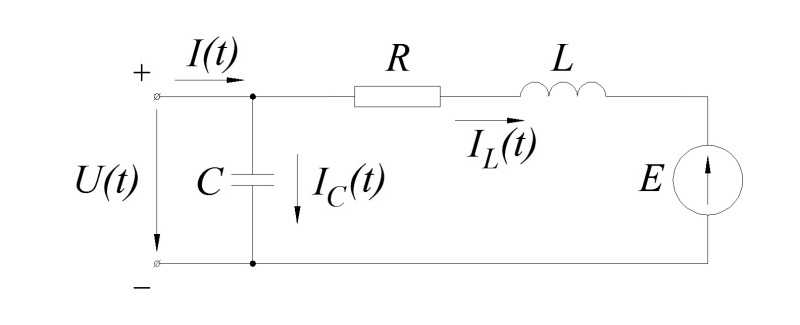
Данная схема описывается системой из трех уравнений:

Цепь связывает два источника. Первый - неизвестное произвольное напряжение

, второй - идеальный источник постоянной ЭДС

.
Моя задача такова: по известной мощности

найти закон

.
Я решил действовать вот так:
Найдем для этого выражение для тока

. Решением первого уравнения будет:

(4)
где

Подставляя (2) и (4) в (3) получим выражение для тока источника

:

. (5)
Теперь остается умножить уравнение (5) на

и решить получившееся уравнение (см. начальный пост) относительно

.